Hola, tengo un problema con este ejercicio y es que no logro ver con cual serie compararla. Ya intente compararla con algunas que he visto pero no llego a nada. Les agradezco si me pueden tirar algún pique para el ej.
El problema por el que les hablo me ha pasado en varios ejercicios y me parece que no soy el único que le ha pasado, no se si pueden darnos alguna lista de las series mas comunes que se usan para los distintos criterios (no se si hay forma de hacer eso) o si existe alguna forma de pensarlo que no he visto, o si es pura intuición.
Saludos.
Hola Facundo. No sé si hay algo así como una lista de series más comunes para comparar. Lo que te diría es que las series a las que tenés que apuntar es a las conocidas, aquellas cuyo comportamiento ya conocemos (las series geométricas, armónicas, telescópicas...).
Por otra parte, al usar el criterio de comparación, lo que estás comparando son los términos principales, que son sucesiones. Por lo que los resultados que te permitan acotar sucesiones, sirven.
En el caso de la serie que tenés en el ejercicio 2) b), mi sugerencia es que notes que el término principal (que puede escribirse como)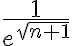 
), decrece rápidamente a 0 ¿Qué quiero decir con "rápidamente"? Que puedo acotarlo superiormente por otra sucesión que también tiende a cero y es término principal de una serie convergente. Para ello, recordá que la cota no tiene por qué valer para todo 
natural sino a partir de un cierto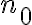 
fijo y elegido convenientemente. Esto te permite concentrarte en buscar una cota que funcione para los grandes. Esto es, pensa en sucesiones que sean menores a la del ejercicio, con tendiendo a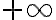 
(y podés aprovechar lo que sabés de orden de infinitos, que considerando que el término principal que tenés es de tipo exponencial, debería ser factible).
Fijate si con esa guía te sale, si no te doy alguna pista más detallada. Pero lo que dije arriba creo que es útil no sólo para ese ejercicio sino para hacer comparación de series en general. Saludos.
Hola, me podes reenviar esta parte? "(que puede escribirse como) \frac{1}{e^{\sqrt{n+1}}), decrece rápidamente".
Sí, no me había dado cuenta que me quedó mal escrito. Ahora lo edité y corregí eso así que debería verse bien en el mensaje original. Gracias.
Puedo decir entonces que e^(n+1)/2 > n^2, a partir de cierto n0 entonces 1/e^(n+1)/2 < 1/n2, y como sabemos que 1/n^2 converge entonces 1/e^(n+1)/2.
No se si ya con eso es suficiente para determinar que converge.
Buenas, yo también estoy medio perdido. Probe decir que eˆ(Sqrt(n+1)) > nˆ2 pero no se cumple, probe con eˆ(Sqrt(n+1)) < n y tampoco.
Efectivamente, la estrategia que plantea Facundo está bien. El problema que tenés, Agustín, es que ninguna de las desigualdades que estás queriendo probar es válida para todo natural. Pero la que nos interesa es que nuestra sucesión está acotada superiormente por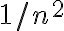 
a partir de algún 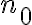. O sea, a partir de dicho valor fijo, la desigualdad debe valer para todo .
Una posible forma de probarlo (que creo es lo que le estaría faltando a Facundo para concluir su prueba, demostrar esa desigualdad) sería comparando los órdenes de infinito de ambas expresiones.