ejercicio 6.c

ejercicio 6.c

de Fernando Gonzalez Estol -
Número de respuestas: 6

Usando a an= 1/(n^2) como contra ejemplo logro darme cuenta de que sqrt(an) no es siempre convergente, pero me gustaría saber si hay alguna forma general de demostrarlo.

saludos!

En respuesta a Fernando Gonzalez Estol

Re: ejercicio 6.c

de Veronica Rumbo -

En realidad, dar un contraejemplo es una forma general de demostrarlo. En todo caso, lo que corresponde hacer es explicar bien por qué la sucesión que das es efectivamente un contraejemplo (es decir, verificar explícitamente que cumple las hipótesis, y que sin embargo la serie de 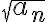\sqrt{a_n} es divergente).

Pero si tu objetivo es refutar la afirmación "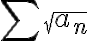\sum \sqrt{a_n} es convergente", basta con dar un contraejemplo ya que la afirmación es (aunque no esté dicho explícitamente) para toda sucesión a_n.

Por otra parte, ahora que encontraste una sucesión tal que 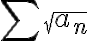\sum \sqrt{a_n} diverge, podría caber preguntarse si son todas así. Es decir, si vale la afirmación "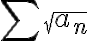\sum \sqrt{a_n} es divergente" para toda sucesión a_n. Nuevamente, para refutar la afirmación basta dar un contraejemplo.

Distinto sería el caso si quisieras probar que una de las afirmaciones es cierta, en ese caso no bastaría con dar un ejemplo que la verifique ya que la afirmación es general y también debe serlo la prueba.

Saludos.
En respuesta a Veronica Rumbo

Re: ejercicio 6.c

de Tomas Galli Alterwain -

Buenas, siguiendo con lo que dice Fernando, entonces esto estaría mal?

En respuesta a Tomas Galli Alterwain

Re: ejercicio 6.c

de Veronica Rumbo -

Buenas, lo dejo por escrito acá de todos modos. El problema con ese argumento está en la afirmación inicial: No es cierto que 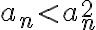a_n < a_n^2. Suponiendo que la sucesión es positiva (lo dice la letra del ejercicio), esa afirmación vale solo si 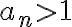a_n > 1. Pero en este contesto estamos trabajando con sucesiones que tienden a cero por lo que tiene sentido asumir justamente lo contrario: que 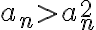a_n > a_n^2, y ahí se rompe el argumento.
En respuesta a Veronica Rumbo

Re: ejercicio 6.c

de Facundo Campal Caputti -

Hola, entiendo intuitivamente que an2  < an pero no se me ocurre como probarlo.

Mi idea es usarlo para poder comparar ambas series en la parte b) del ejericio 6.


En respuesta a Facundo Campal Caputti

Re: ejercicio 6.c

de Veronica Rumbo -

La clave está en que como la serie 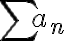\sum a_n converge, sabemos que la sucesión a_n tiende a cero (cuando n \rightarrow +\infty).

Entonces es posible afirmar que a partir de cierto 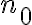n_0, los términos de la sucesión van a ser todos menores a 1.

Y dado 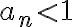a_n < 1 (positivo) se tiene que  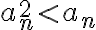a_n^2 < a_n, que se obtiene de multiplicar ambos lados de la desigualdad por a_n (por ser a_n positivo se preserva la desigualdad).