Foro Práctico 4

La clave está en que como la serie 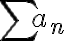$\sum a_n$ converge, sabemos que la sucesión $a_n$ tiende a cero (cuando $n \rightarrow +\infty$).

Entonces es posible afirmar que a partir de cierto 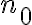$n_0$, los términos de la sucesión van a ser todos menores a 1.

Y dado 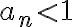$a_n < 1$ (positivo) se tiene que  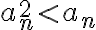$a_n^2 < a_n$, que se obtiene de multiplicar ambos lados de la desigualdad por $a_n$ (por ser $a_n$ positivo se preserva la desigualdad).