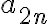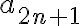Hola Ezequiel. la idea es que demuestren "formalmente" por qué converge. La buena noticia es que si estás bien encaminado con la idea intuitiva de por qué lo hace, pasar de ahí a una "verdadera" demostración no está tan lejos. No quiere decir que sea fácil hacer ese salto pero justamente estos ejercicios son una buena instancia para agarrarle la mano.
No sé cual es tu intuición de por qué es cierto, quizás sea una idea gráfica. Capaz, a partir de la noción de punto de aglomeración (cada uno de esos límites de subsucesiones son puntos de aglomeración de la sucesión).
Para formalizar un poco, lo primero es tener claro qué queremos probar: Que existe el límite de  (llamémosle
(llamémosle  ). Esto tiene varias formulaciones alternativas: por ejemplo que la sucesión sea de Cauchy, o que toda subsucesión de
). Esto tiene varias formulaciones alternativas: por ejemplo que la sucesión sea de Cauchy, o que toda subsucesión de  converge a
converge a  . Dada la información que nos dan en la letra, parece un buen camino ir por acá. Entonces, un camino posible a seguir es ese: Considerar una subsucesión genérica y probar que converge a
. Dada la información que nos dan en la letra, parece un buen camino ir por acá. Entonces, un camino posible a seguir es ese: Considerar una subsucesión genérica y probar que converge a  .
.
¿Cómo podemos hacer esto? Imaginemos por un momento que nuestras hipótesis son un poco más fuertes: no sólo sabemos que 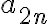 ,
, 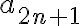 y
y  convergen sino que también sabemos que su limite es
convergen sino que también sabemos que su limite es  (esta condición, si bien es cierta y necesaria, no fue probada aún. Pero asumamos momentáneamente que sí). Con esta info adicional, deberías poder probar que la subsucesión genérica tiende a
(esta condición, si bien es cierta y necesaria, no fue probada aún. Pero asumamos momentáneamente que sí). Con esta info adicional, deberías poder probar que la subsucesión genérica tiende a  (básicamente, todos los términos de tu subsucesión genérica están o bien en
(básicamente, todos los términos de tu subsucesión genérica están o bien en 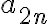 o bien en
o bien en 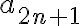 ). Y en consecuencia
). Y en consecuencia  converge.
converge.
Para terminar la demostración faltaría hacernos cargo de lo que supusimos sabido: Que el límite de las 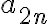 ,
, 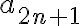 y
y  es
es  . Una posibilidad para ello es ir por absurdo. Si
. Una posibilidad para ello es ir por absurdo. Si 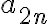 y
y 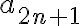 tuviesen límites distintos,
tuviesen límites distintos,  no podría converger.
no podría converger.
Lo que escribí fue una guia de como podría ser la demostración. FIjate que el razonamiento fue un poco "de atrás hacia adelante". Eso es algo que se hace a veces al demostrar. Si necesito alguna hipótesis que no tengo (pero que parece verosimil), la asumo momentaneamente para terminar la demostración, y después la pruebo. En realidad si fuésemos a hacer la demostración entera de un modo más lineal, podría resumirse en dos grandes pasos:
- Probar que
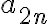 ,
, 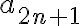 y
y  tienden a un mismo límite
tienden a un mismo límite 
- Sabiendo lo anterior, probar que toda subsucesión de
 también tiende a
también tiende a 
Me limité a esbozar un camino posible con la intención de que vos intentes escribir bien cada uno de estos pasos, y lo seguimos viendo. Si ves que en algun momento no sabés como probarlo, preguntalo y la seguimos. Y si querés mandar por acá una foto de la demostración terminada cuando esté, hacelo también y la vemos.
Saludos