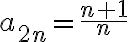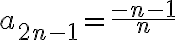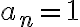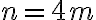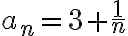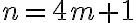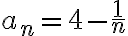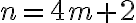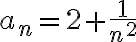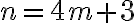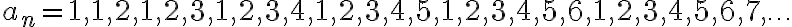Buenos días, no se me ocurre que forma tiene que tener la sucesión para que tenga puntos de aglomeración, desde ya muchas gracias.
Buenas, me sumo a la duda. En realidad tengo algunas ideas pero no se como escribirlas, importa eso?
Por ejemplo, en la parte uno (que también sirve para la parte dos) se me ocurrió que podría ser an=n/(el numero de entrada), y mis subsucesiones serian los múltiplos del punto de aglomeración al que quiero llegar. De esa forma, si el punto de aglomeración es 3, mi subsucesión seria (3,6,9,12,15...) y ank = (3/1; 6/2; 9/3; 12/4; 15/5;...). El problema es que no se como escribir lo de la división por el numero de entrada.
Se que es confuso, pero es la única forma que se me ocurrió, me gustaria saber si hay alguna forma mas sensilla o si esa es correcta.
Gracias, saludos.
Buenas,
como dice el ejercicio 6, un punto es de aglomeración de una sucesión si existe una subsucesiòn que converge a este punto.
Un ejemplo de un punto de aglomeración es el límite de una sucesión convergente, porque sabemos que toda subsucesión de una sucesión convergente a  , converge a
, converge a  también.
también.
Consideremos la sucesión 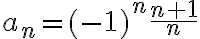 observar que:
observar que:
La subsucesión 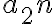 converge a
converge a  y
y 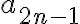 converge a
converge a 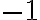 por lo tanto
por lo tanto  y
y 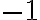 son puntos de acumulación de la sucesión
son puntos de acumulación de la sucesión  .
.
En particular, en el ejercicio 6 les piden construir una sucesión cuyos puntos de acumulación sean 1,2,3,4. Hay varias sucesiones que cumpliran esto, por ejemplo:
También podemos definir una sucesión 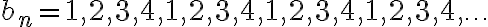 , ¿cómo escribirian el término enesimo de
, ¿cómo escribirian el término enesimo de 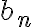 ?
?
¿Con esto pueden hacer la parte b)?
Hola estaba haciendo el ejercicio b
Y se me ocurrio esto, osea utilizar una sucesion que tenga un doble sub indice, elijo el punto de aglomeracion k y luego pruebo con todos los naturales.
a_sub(n_sub(k)) = kn - (kn -k)
No se si se enteinde la idea, y tampoco se si es correcto, saludos y muchas gracias
Diego
Para construir una sucesiòn que aglomere en todos los naturales, podemos intentar copiar la idea de la sucesión de la parte anterior. Es decir, una sucesiòn que haga lo siguiente: recorrer los naturales de 1 a n, luego de 1 a n+1, y así sucesivamente, pasando por todos los naturales infinitas veces.
Sin embargo, es un poco molesto escribir esto de forma compacta (a pesar de que la idea es correcta).
Dado n, definimos 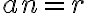 si
si  con
con  algún primo y
algún primo y 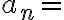 0 en caso contrario.
0 en caso contrario.
Dado que los números primos son infinitos, y la descomposiciión de un natural en productos de primos es única, necesariamente  deberá pasar por todos los naturales infinitas veces. Por ejemplo, dado
deberá pasar por todos los naturales infinitas veces. Por ejemplo, dado 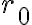 natural, una subsucesión que converge a
natural, una subsucesión que converge a 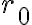 es la correspondiente a los números
es la correspondiente a los números 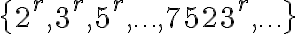 .
.