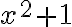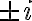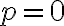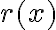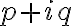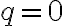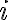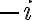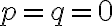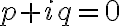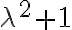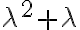Buenas noches,
Situándonos en la resolución de este ejercicio, ecuación diferencial lineal de segundo orden no homogénea, a la hora de aplicar el método de selección para determinar Yp(x), me encuentro con qué a la hora de descomponer r(x) según la fórmula de la hipótesis (la que hay que elegir, p, A(x), B(x) y q apropiadamente) esta se descompone de tal manera que:
(p= 0, A(x) = r(x) , q = 0, B(x) = 0)
Uno por inercia diría bueno p + iq y p - iq no son raíces de la ecuación característica, porque en este caso de la ecuación no salen raíces complejas. (Raíces de la ecuación característica: 0 y 1). Entonces se procede a utilizar la primera forma de Yp(x) del método de selección, resultando en un polinomio genérico de 2do grado. Y así lo resolví, y llegué a la solución.
Pero más tarde me fijé en las notas de Eleonora, y se aclara que en caso de que q = 0 y p sea raíz simple de la ecuación característica, que lo es, estamos habilitados a utilizar la "segunda forma" de la solución Yp(x), siendo igual a la anterior pero, multiplicada por x, quedando un polinomio de 3er grado sin término independiente.
E intenté resolverlo de esta forma y aparecen problemas a la hora de despejar los coeficientes de este polinomio, dado que r(x) es de segundo grado. Se obtienen más de un valor para cada coeficiente, dándome a entender que es un sistema incompatible.
Nada, es una duda..., algo quisquillosa se podría decir, pero aún así me gustaría saber por qué esto sucede, dentro de lo posible. Muchas gracias.