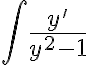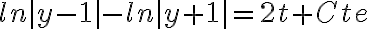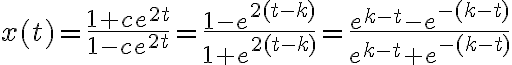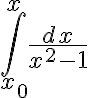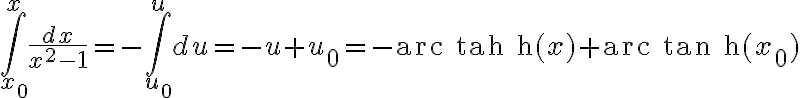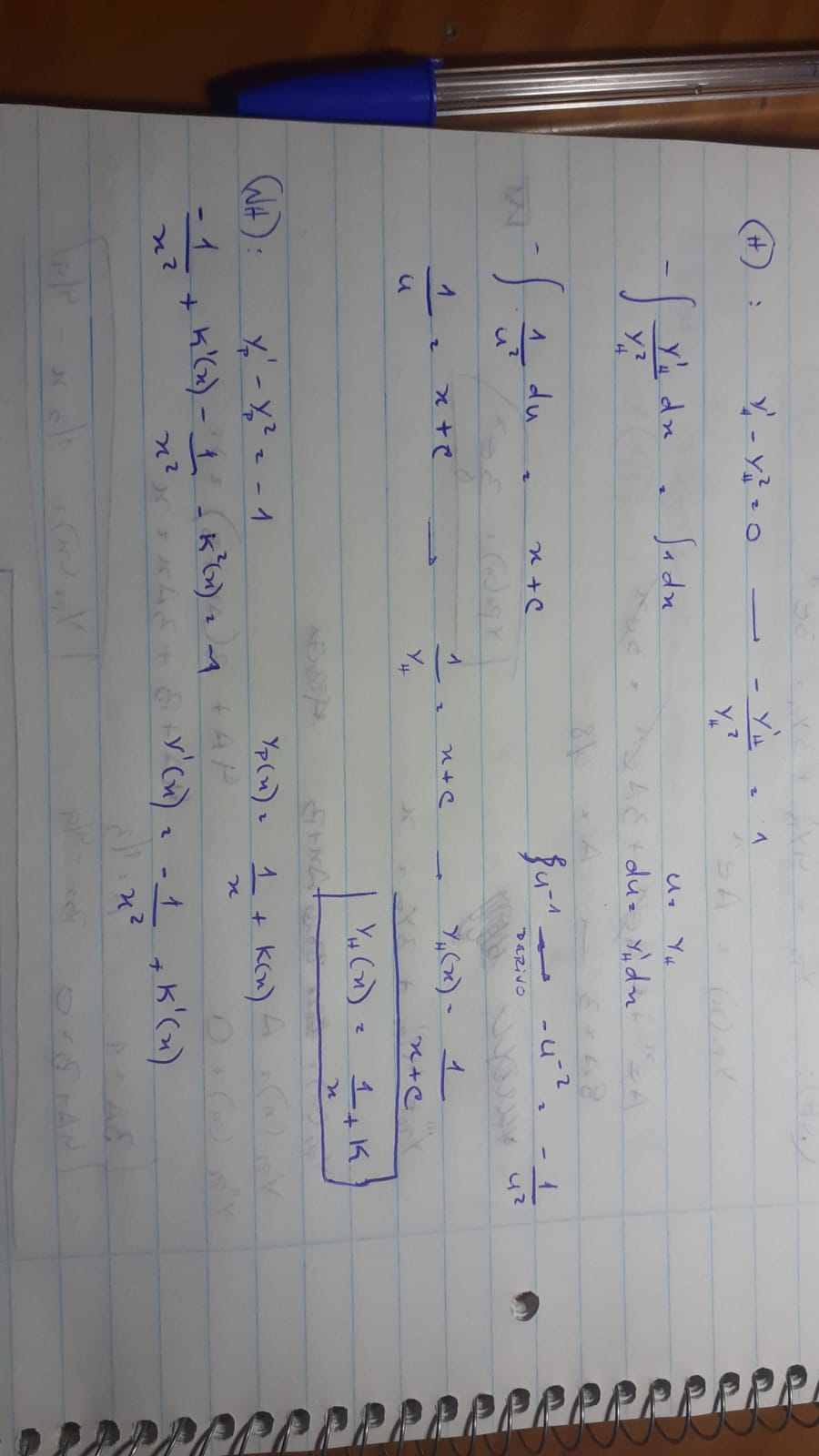
Hola! En ese ejercicio, por qué no tomas la función (y^2)+1 y la función 1 y haces variables separables? Escrito como en el teórico, y' = F(y(t))H(t) siento F(y) y^2 +1 y H(t)= 1.
Hola,
más allá de lo que propone Valentina, que me parece bien, te comento porque uno no esperaría que funcione el método que estas utilizando. El método que estas usando es el método de variación de constante el cuál se sabe que funciona siempre para ecuaciones diferenciales lineales de primer orden, pero esta ecuación diferencial no es lineal por lo cuál no tendría porque funcionar.
Buenas, no se si se siguen contestando dudas de este práctico, pero vengo medio atrasado.
Lo que no entiendo es el resultado que dan en el pdf.
Al separar las variables de la ecuacion 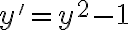 tomando
tomando 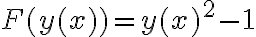 y
y 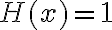
y aplicando integral en ambos lados de la ecuacion me queda
Luego resolviendo la integral por fracciones simples llego a que
Que no parece tener nada que ver con el resultado que publicaron.
Hola!! Vas bien. Acordate que cuando resolves la ecuación diferencial, las soluciones que obtenes son funciones. Es decir, en este caso, una función y(t) tal que si la derivo una vez, es igual a la función al cuadrado menos uno. Así que tenés razón, tenés que despejar y. (Aunque según ví en el teórico, la expresión como la pusiste ya es solución y hay veces que no se puede o es muy trabajoso despejar y).
Lo que yo te recomiendo para despejar y es usar la inversa de logaritmo, e. Hacé e a cada parte de la igualdad y luego como e^log(x) = x (faltaría algún valor absoluto pero vos vas viendo), ya tenés el "y" solito para despejar.
Otra propiedad que te puede ser útil: e^(x+y)= e^x *e^y .
Cualquier cosa si te trancas volvé a preguntar. Saludos!!
Muchas gracias ya llegue al resultado correcto. Creo que me había "asustado" cuando leí en la resolución que pusieron algo sobre la tangente hiperbólica jaja. Lo no entendía tampoco, es a que se referían con lo de las soluciones constantes. Pero claro, luego me di cuenta que si en el tiempo cero y(0) vale 1 o -1, entonces la solución va a ser constante para todo t. Por tanto todas las soluciones pueden ser de de dos formas dependiendo de que valor toma y en t=0: o son constantes, o son de la forma general que aparece en la resolución. Lo de la tan hiperbólica igual sigo sin entenderlo mucho de donde lo sacaron...en fin, gracias por la orientación!
Me alegro que te haya salido! Lo de tangente hiperbólica te digo mas o menos que entendí yo. Primero hace x(0) y despeja c y le queda c = x0−1/ x0+1. Luego la parte de que c = e^-2k surge de las cuentas que hiciste al despejar y si en vez cambiar la constante k que sale de la integral por una constante cualquiera c le haces las cuentas bien como corresponde. Hasta ahí llegue, luego no entendí mas nada porque no supe que hacer con los unos jej pero tal vez te sirva. Saludos!! :D
Hola,
Me parece perfecto que discutan entre ustedes. Como se venían respondiendo bien preferí no decir nada. Veo que se respondieron entre ustedes lo importante. El comentario que hace la solución sobre tangente hiperbólica es menor, pero si les interesa les comento:
La solución observa que si 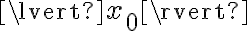 entonces
entonces 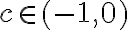 . Si no me equivoco aquí hubo en error, en realidad si
. Si no me equivoco aquí hubo en error, en realidad si 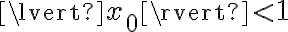 entonces
entonces 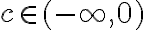 . De todas formas lo que sigue comentando la solución esta bien. Lo que hace la solución es aprovechar que
. De todas formas lo que sigue comentando la solución esta bien. Lo que hace la solución es aprovechar que  es negativo para estos casos y entonces se puede escribir
es negativo para estos casos y entonces se puede escribir 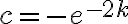 con
con 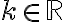 . Entonces la solución se puede reescribir asi:
. Entonces la solución se puede reescribir asi:
y esto último es, por definición, es 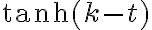 . Algo similar se puede hacer para cuando
. Algo similar se puede hacer para cuando 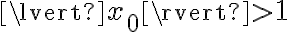 . Esto es lo que comenta la solución.
. Esto es lo que comenta la solución.
------------------------
Estos trucos de tangente hiperbólica también se pueden ver por otros lados, capas que les resulta más claro:
Uno desea integrar
Si 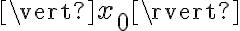 entonces
entonces  al menos para
al menos para  cercano a cero (por continuidad). Les recuerdo que
cercano a cero (por continuidad). Les recuerdo que 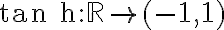 es una biyección. Como
es una biyección. Como  puedo hacer el siguiente cambio de variable
puedo hacer el siguiente cambio de variable 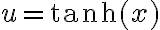 , con esto
, con esto 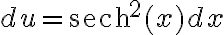 (ver alguna tabla de derivadas), además si uso que
(ver alguna tabla de derivadas), además si uso que 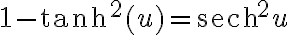 entonces
entonces
esta integral era igual a  entonces despejando
entonces despejando 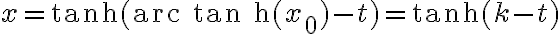
----------------
Dos cosas más, en las cuentas anteriores uso 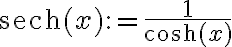 solo por comidad.
solo por comidad.
Por último, insisto que solo son cuentas, la solución escrita solo con exponenciales ya esta bien
Saludos
Gracias!! :D