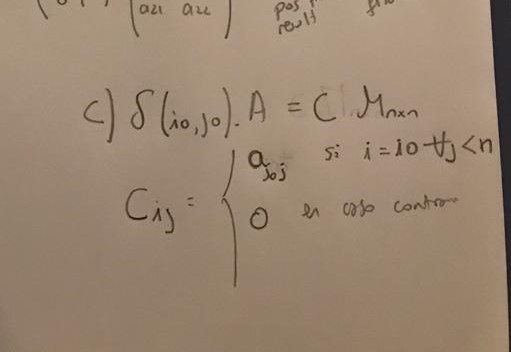Buenas, estoy teniendo dificultades para entender la letra del ejercicio.
Por lo que entiendo, nos da un elemento \( \delta(i_0,j_0) \in M_{n \times n} \) (Una matriz cuadrada de \( n \) filas y \( n \) columnas)
Y dice que sus entradas valen \( 1 \) si el \( i \) y el \( j \) son \( i_0 \) y \( j_0 \) y \( 0 \) en otro caso.
No entiendo bien como está definiendo esta matriz ¿Es una matriz llena de ceros y un único elemento 1 o hay más \( \delta(i_0,j_0)\ \)?
Cualquier idea ayuda, gracias :D
Hola Daniel,
Efectivamente, la matriz $$\delta(i_{0},j_{0})$$ es una matriz llena de ceros y solamente un 1 en la posición $$(i_{0},j_{0})$$. Para resolver el ejercicio te recomiendo plantear los casos en que n es un número definido (puede ser 2, 3 o 4) y ver que sucede con los productos que se plantean, para luego intentar descifrar que implican dichos productos para un n genérico. A modo de ejemplo, la matriz $$\delta(1,2)$$ tomando $$n=3$$ sería de la forma
$$\left(\begin{array}{ccc}0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right)$$
Puede ser útil también leer esta consulta, ya que una compañera ya había preguntado por este ejercicio: https://eva.fing.edu.uy/mod/forum/discuss.php?d=176532
Cualquier cosa preguntá de nuevo.
Saludos
Hola, ahora entendí la notación, sin embargo no termino de entender que hay que hacer, existe la posibilidad de subir una resolución escrita o algo? gracias
Por lo que entendí hay que multiplicar una matriz por otra cualquiera llamada \( \A \) y ver que pasa. Pero no estoy 100% seguro por eso espero la respuesta del profe.
Y estoy de acuerdo con que debería haber alguna resolución para tomar como buen ejemplo.
Hola Daniel,
Tanto tu razonamiento como la conclusión a la cual llegaste son correctas. La idea del ejercicio es justamente esa, plantear una matriz genérica (en principio es útil trabajar con $$n=3$$) y realizar los productos $$A\delta(i_0,j_0)$$ y $$\delta(i_0,j_0)A$$.
Una vez que se haya realizado esto para $$\delta(1,1)$$ y $$\delta(1,2)$$ resulta más fácil ver que, de forma general, el producto $$A\delta(i_0,j_0)$$ resulta en una matriz cuya j-ésima columna será igual a la i-ésima columna de la matriz A mientras que todas las demás entradas son cero. Por otro lado, el producto $$\delta(i_0,j_0)A$$ resulta en una matriz cuya i-ésima fila es igual a la j-ésima fila de la matriz A, mientras que todas las demás entradas son cero.
Realizar el producto de forma genérica para matrices de nxn y llegar a esa conclusión es el fin del ejercicio.
Saludos
Gracias por la respuesta, perdón que no vi que ya gabía habierto el tema en este ejercicio.
Ahora me surge otra duda:
Sabiendo que tengo que multiplicar mi matriz \( \delta (1,1) \) por una matriz \( A \) lo que veo es que voy a obtener es una matriz con una única fila de tamaño \( n \) y el resto de las filas nulas.
Y si multiplico \( A \) por la matriz \( \delta (1,1) \) (O sea que cambio el orden) veo que se obtiene una matriz con un única columna de tamaño \( n \) y el resto de las columnas son nulas.
Para un \( n=3 \) quedaría así el producto de \( \delta (1,1) \) y \( A \)
\( \left(\begin{array}{ccc}a_{11} & a_{12} & a_{13}\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right) \)
Algo similar pasaría en la parte b) pero para la ubicación sería \( \delta (1,2) \) entonces quedaría solo la segunda fila con entradas de \( A \) y cambiando el orden del producto la segunda columna con entradas de \( A \)
No se como describiría todo eso bien, lo mismo para un \( \delta_{(i_0,j_0)} \) quedaría siempre la columna y fila donde se encuentre el valor 1 en la matriz \( \delta_{(i_0,j_0)} \)
¿Está bien solo con entenderlo o hay que hacer una demostración?
En la parte c) describi la solución de la siguiente forma, está bien ?
Gracias!
Hola Enrique, queda eso si. El \( \forall j<n \) no iría, se sobreentiende que es \( \forall j\) (igual en todo caso sería \(<=n\) ).
Saludos
Hola Daniel, lo que planteas está muy bien. Ahora para el caso general, pensá qué fila (o columna) "copia" de A y qué fila (o columna) la "pega", y a partir de ahí ver cómo escribir la matriz resultante.
Saludos