Hola, tanto la Parte a) como la b), no me arrojan como resultado algo similar al solucionario de este práctico. Agradezco me contesten en que me estoy equivocando.
Gracias, Saludos.
Hola! Si te estás equivocando no se, pero si en vez de sustituir y'(x) por du/dx , pones y'(x) = ( u(x)*x)' y haces los cálculos queda bien. Lo que sería B(x) es -1/x y A(u) es u^2(x) (según yo).
Creo que estás tomando A y B como escalares y según entendí son funciones.
Saludos!
Hola, en realidad es lo mismo, lo único que cambié fue la notación, pero más allá de eso, M. Fiori en la clase de Variables Separables de
Open-fing aclara sobre las notaciones y hace notar sobre las que en mi caso use.
A y B no son los del ejercicio, solo me quedo igual a la notación del ejercicio, podrían haber sido C y D, solo las use para resolver la integral por Fracciones Simples.
Igual gracias por contestar.
Paso una parte del Teórico que use.
Ah! Si primero haces la sustitución y luego haces ese método con u'(x) también llegas a la respuesta pero creo que eso no es lo que queres hacer.
Igualmente si llegas a resolverlo así como lo estas haciendo decime que hiciste.
Y de nada :D.
Buenas!! Yo pude llegar al resultado, con la única diferencia de que k me quedó positiva. Es una solución correcta también? Cómo lo puedo solucionar?
Muchas gracias!
Hola Melina. Si bien no está dicho explícitamente, en la solución sobreentendimos que 
es una constante real arbitraria. Por lo que la expresión que vos tenés también es correcta (digamos, si tenés una solución con por ejemplo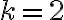 
, se correspondería con la que tiene 
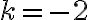en la hoja de resultados).
Como respuesta más general aún, siempre que tengas la duda "¿Será correcta esta solución de la ecuación diferencial que acabo de hallar?", podés resolverla derivando tu candidata a solución las veces que sea necesario y sustituyendo en la ecuación original. A veces es tedioso pero recomiendo hacerlo. Especialmente cuando algo no te cierra, como ahora.
Saludos