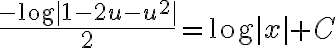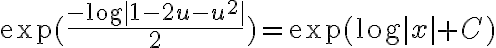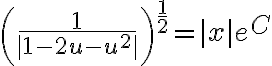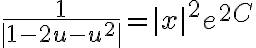Buenos días, he hecho el cambio de variable correspondiente y no me a simplificado el problema, me gustaría saber como lo han encarado y que les a salido.

Sí, es por ahí. No queda especialmente breve y amigable pero está bien.
Buenas tardes. Me podrías dar alguna idea de como despejar u(x) a partir de eso ?
Lo intenté pero fallé :(.
Igualmente, supongo que es primero poner lo que este multiplicando al logaritmo como un exponente, luego hacer e a la todo eso, después resolver la ecuación con u(x) y debería quedar.
Muchísimas gracias!
Está bien la idea, y hay que tener cuidado al operar. Tomando como punto la solución a la que llegó Valentina, es decir
[Editado: había un error al copiar la primera ecuación]
lo que estás proponiendo sería aplicar una función exponencial de ambos lados, con lo cual quedaría
siendo 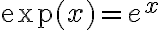 . Propiedades de potencia y logaritmo mediante, el lado derecho de la igualdad entonces puede escribirse como
. Propiedades de potencia y logaritmo mediante, el lado derecho de la igualdad entonces puede escribirse como 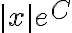 . El lado izquierdo queda
. El lado izquierdo queda 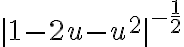 y la igualdad anterior
y la igualdad anterior
O bien, equivalentemente (elevando al cuadrado ambos miembros teniendo en cuenta que ambos son positivos)
Desde ahí, tienen un polinonio de segundo grado que se puede despejar (tomando  como variable).
como variable).
Hola, buenas tardes, yo había llegado a lo mismo que pusieron acá, pero llevo un rato dándole vueltas y no termino de entender como despejar u en esa ecuación.
Fijate que la ecuación la podés escribir como 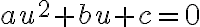 , donde
, donde 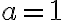 ,
, 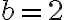 y
y 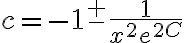 .
.
Con esos coeficientes para el polinomio de segundo grado, podés despejar  (que te va a quedar en función de
(que te va a quedar en función de  ya que
ya que  aparece en el término independiente, y eso está bien.
aparece en el término independiente, y eso está bien.
Por otro lado notar que el uso de 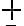 es para abreviar la escritura pero lo que hay son dos casos, uno con el + y otro con el -, correspondientes a soluciones distintas (si tuviésemos condiciones iniciales tendríamos que elegir un signo según conveniencia).
es para abreviar la escritura pero lo que hay son dos casos, uno con el + y otro con el -, correspondientes a soluciones distintas (si tuviésemos condiciones iniciales tendríamos que elegir un signo según conveniencia).
(Editado para corregir un error arrastrado del post original)
En la parte donde Veronica nos muestra como despejar u, no está faltando un menos en el lado izquierdo?? De esa manera, luego de todo el proceso nos quedaría 1/x^2 del lado derecho... Estoy en lo cierto? Muchas gracias!!
Tenés razón! Se me escapó un - al principio y eso cambia las cuentas. Ya lo edito. Gracias
De nada! Gracias a vos!!