Foro Práctico 1.

No es un ángulo desconocido, sino que es un parámetro de integración. 

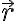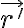El ángulo θ al que hace referencia Tomas (que es el ángulo entre los vectores $\vec{r}$ y $\vec{r'}$, es el ángulo de coordenadas esféricas que, junto a un ángulo φ de revolución, te permite recorrer toda la superficie esférica, y son las variables sobre las que hay que integrar para obtener el potencial. O sea, para una pareja θ, φ me paro en un punto de la superficie, y a medida que ellos varían, de 0 a π el ángulo θ, y de 0 a 2π el ángulo φ, recorro toda la superficie esférica. Son las variables que permiten parametrizar la posición 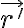$\vec{r'}$ de las cargas que generan el potencial. Al integrar en esos ángulos considero la contribución de todas las cargas, y el resultado de la integral no depende de ellos. O sea, 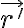$\vec{r'}$ recorre toda la superficie esférica mientras 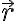$\vec{r}$, el punto en el que quiero calcular el potencial, se puede considerar fijo. El resultado dependerá de este último, no del primero

Pero además, el potencial al que se quiere llegar, no depende de ningún ángulo, porque al tener el problema simetría esférica, el potencial solo depende de r, la distancia del punto del espacio en que se quiere calcular el potencial al centro de la esfera,.Esto es porque todos los puntos que tienen la misma distancia all centro de la esfera, están en las misma condiciones físicas. Entonces el potencial no puede depender de ningún ángulo.