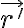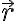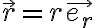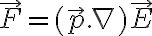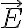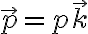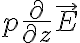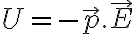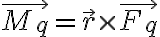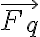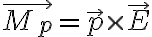Foro Práctico 1.

En la parte a podés hacer el gradiente del potencial del dipolo o directamente aplicar la fórmula del campo eléctrico de un dipolo, que es la ecuación 2.36 del Reitz, Milford, Christy https://drive.google.com/drive/folders/18zEbJ_aqHsga8ROIixM2Aa1kDQ46q_t8?usp=sharing. Esta ecuación es menos el gradiente del potencial del dipolo, que es la ecuación 2.39 de ese libro. En esta expresión, 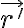$\vec{r'}$, que es la posición del dipolo, vale 0. Y 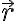$\vec{r}$, que es la posición donde se evalúa, es la posición de la carga, que en coordenadas esféricas es $\vec{r} = r \vec{e_r}$.

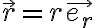En la parte b, tenés que calcular por un lado la fuerza que hace el dipolo sobre la carga y por otro la que hace la carga sobre el dipolo y ver que son iguales y opuestas. La fuerza que hace el dipolo sobre la carga es muy fácil porque es la carga multiplicada por el campo hallado en la parte a. 

La fuerza que hace la carga sobre el dipolo se puede calcular de dos formas distintas. Una es la que aparece en la clase 3 de OpenFing (minuto 1:10): 

$\vec{F}=( \vec{p}.\nabla) \vec{E}$

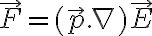
donde 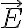$\vec{E}$ es ahora el campo externo que actúa sobre el dipolo, en este caso el de la carga puntual. Como 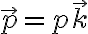$\vec{p} = p \vec{k}$ esto queda $p \frac{\partial}{\partial z} \vec{E}$. 

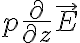La otra forma es que la fuerza es menos el gradiente de la energía, y la energía del dipolo en un campo externo es: 

$U = - \vec{p}. \vec{E}$

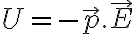
ecuación 2.44 del Reitz, Milford, Christy. 

Para la parte c de nuevo hay que calcular el momento de la fuerza del dipolo sobre la carga, y de la carga sobre el dipolo y ver que son iguales y opuestos. Para el momento de la fuerza del dipolo sobre la carga (respecto al origen de coordenadas que es donde está el dipolo) será: 

$\vec{M_q} = \vec{r} \times \vec{F_q}$

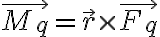
donde 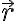$\vec{r}$ es de nuevo la posición de la carga y 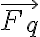$\vec{F_q}$ es la fuerza del dipolo sobre la carga calculada en la parte b. 

El momento de la carga sobre el dipolo se calcula de acuerdo a la ecuación que aparece en el minuto 1:15:25 de la clase 3 de OpenFing: 

$\vec{M_p}= \vec{p} \times \vec{E}$ 

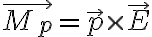
donde 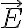$\vec{E}$ es de nuevo el campo eléctrico de la carga.