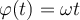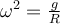Hola Margaret, buen día.
Nos piden que la partícula tenga un movimiento circular uniforme relativo al aro. Para ello debemos ver que la coordenada que describe la posición relativa de la partícula en el aro 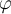 debe satisfacer que:
debe satisfacer que: 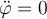 o lo que es igual
o lo que es igual 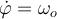 con
con 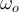 constante y por ende
constante y por ende 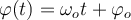
De imponer esto en la ecuación de movimiento se obtiene que: 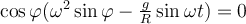
Debemos igualar tanto el argumento de los senos como las constates multiplicativas:
Espero haber aclarado tu duda!