Foro Práctico VI

Hola Romina,

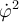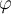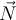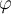en la parte d) de este ejercicio necesitamos conocer $\dot \varphi ^2$ en función de $\varphi$ mientras el disco se desliza, de manera de estudiar luego, a partir de la primera cardinal al disco según la dirección normal, cómo varía la reacción normal $\vec N$ con $\varphi$ y obtener el ángulo 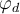$\varphi_d$ donde se anula y se produce el desprendimiento.

A efectos de hallar la función 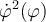$\dot \varphi ^2(\varphi)$ mientras el disco se desliza, se necesita conocer 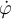$\dot \varphi$ en el comienzo del deslizamiento (es decir 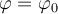$\varphi=\varphi_0$) que es igual al valor que tenía inmediatamente antes de comenzar a deslizarse: si no fuera así, se produciría un salto en la velocidad del centro del disco, lo cual a su vez corresponde a una aceleración infinita en un tiempo muy corto (y por lo tanto a una fuerza infinita actuando durante un tiempo muy corto, lo cual es propio de fenómenos impulsivos como colisiones que habrás visto en Física 1).

En resumen: si el rígido o partícula no experimenta una colisión (se le aplica un golpe), es esperable que la velocidad (lineal, angular) no sufra un salto (puede en cambio sí producirse un salto en la aceleración por discontinuidad de una fuerza, ver por ejemplo 8.5.3 en los Apuntes 2010).

Saludos,

Ariel.