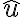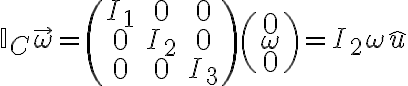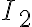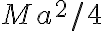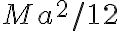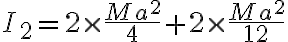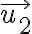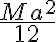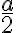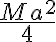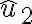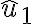Hola, intenté hacer la primera parte de este ejercicio calculando el momento de inercia de una barra en su centro de masa y luego usando steiner para obtener el momento en C, y luego multiplicando por 4, por las cuatro barras.
Mirando la solución no logro entender por qué aplica steiner dos veces para calcular el momento de incercia total de las barras.