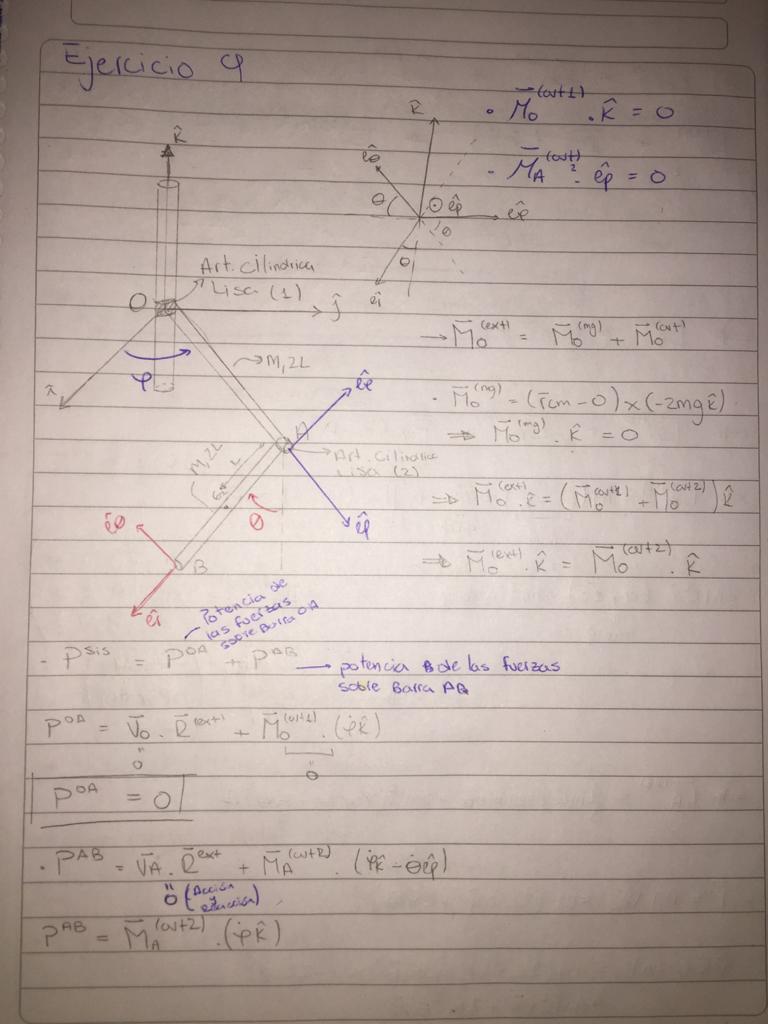
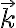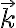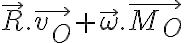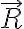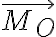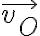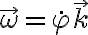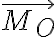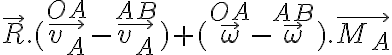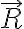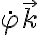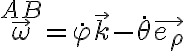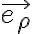En relación al momento lo que hay que tener en cuenta es que para demostrar que se conserva la componente según 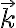 del momento angular se aplica la segunda cardinal al sistema completo formado por ambas barras. Eso es lo que se conserva: la componente del momento angular del sistema formado por ambas barras, no el de cada barra por separado. En la segunda cardinal aparecen solo los momentos de fuerzas externas. Las fuerzas internas no aparecen en las cardinales por acción y reacción (en la demostración de las cardinales se anulan). Por lo tanto en la cardinal al sistema de dos barras solo se consideran los momentos de los pesos de cada barra y el momento de la articulación en O. El momento de la articulación en A no aparece en esa cardinal porque es una fuerza interna (de interacción entre las barras).
del momento angular se aplica la segunda cardinal al sistema completo formado por ambas barras. Eso es lo que se conserva: la componente del momento angular del sistema formado por ambas barras, no el de cada barra por separado. En la segunda cardinal aparecen solo los momentos de fuerzas externas. Las fuerzas internas no aparecen en las cardinales por acción y reacción (en la demostración de las cardinales se anulan). Por lo tanto en la cardinal al sistema de dos barras solo se consideran los momentos de los pesos de cada barra y el momento de la articulación en O. El momento de la articulación en A no aparece en esa cardinal porque es una fuerza interna (de interacción entre las barras).
En definitiva, la articulación en A si ejerce momento según 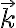 , pero por acción reacción, el momento sobre la barra OA es igual y opuesto al momento sobre la barra AB. Y en la segunda cardinal al sistema formado por las dos barras esos momentos se anulan.
, pero por acción reacción, el momento sobre la barra OA es igual y opuesto al momento sobre la barra AB. Y en la segunda cardinal al sistema formado por las dos barras esos momentos se anulan.
Algo parecido pasa en el teorema de la energía. Lo que voy a hacer a continuación es repetir el desarrollo que aparece en la solución de este ejercicio subida al EVA. Para demostrar que se conserva la energía hay que demostrar que todas las fuerzas son conservativas o de potencia nula. Los pesos son conservativos, y las fuerzas internas de los rígidos son de potencia nula. Hay que ver que pasa con la potencia de las articulaciones.
Para la articulación en O es más fácil, porque la potencia de esa reacción es:
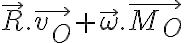
donde 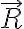 y
y 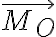 son la resultante y el momento de las fuerzas ejercidas por la articulación en O;
son la resultante y el momento de las fuerzas ejercidas por la articulación en O; 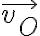 es la velocidad del punto O (como perteneciente a la barra OA, que es sobre la que actúa la fuerza de la articulación), que es 0 porque el punto O está fijo; y
es la velocidad del punto O (como perteneciente a la barra OA, que es sobre la que actúa la fuerza de la articulación), que es 0 porque el punto O está fijo; y 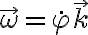 es la velocidad angular de la barra OA. Luego aparece el producto escalar de
es la velocidad angular de la barra OA. Luego aparece el producto escalar de 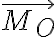 y
y 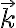 , que es cero porque la articulación es lisa (y
, que es cero porque la articulación es lisa (y 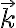 es el eje de la articulación). Entonces esa articulación es de potencia nula.
es el eje de la articulación). Entonces esa articulación es de potencia nula.
Para la articulación en A hay que considerar la potencia de las fuerzas actuando sobre la barra OA, y las de su reacción actuando sobre AB, que por acción y reacción son iguales y opuestas. Luego la potencia total será (aplicando la misma fórmula de antes dos veces, pero ahora en el punto A):
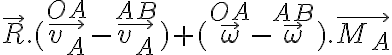
donde 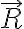 y
y  son la resultante y el momento de las fuerzas ejercidas por la articulación en A ahora y los superíndices OA y AB se refieren a velocidad lineal o velocidad angular de la barra OA y la AB, respectivamente. El signo de - aparece por acción y reacción. El primer término es nulo porque la velocidad del punto A es la misma como perteneciente a ambas barras (las barras están unidas en A). La velocidad angular de la barra OA es la que se escribió antes
son la resultante y el momento de las fuerzas ejercidas por la articulación en A ahora y los superíndices OA y AB se refieren a velocidad lineal o velocidad angular de la barra OA y la AB, respectivamente. El signo de - aparece por acción y reacción. El primer término es nulo porque la velocidad del punto A es la misma como perteneciente a ambas barras (las barras están unidas en A). La velocidad angular de la barra OA es la que se escribió antes 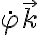 . Y la de la barra AB es
. Y la de la barra AB es 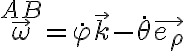 . Así que la diferencia de las velocidades angulares queda según
. Así que la diferencia de las velocidades angulares queda según 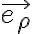 , que es el eje de la segunda articulación, que también es lisa, por lo que su momento según esta dirección también es nulo. Por lo tanto la articulación en A también es de potencia nula.
, que es el eje de la segunda articulación, que también es lisa, por lo que su momento según esta dirección también es nulo. Por lo tanto la articulación en A también es de potencia nula.