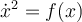Buenas tardes. Viendo la solución de este ejercicio, encontré una parte que no entiendo. Cuando esta calculando la energía cinética de la pieza llega a (Icφ’2)/2,no debería ser dividido 4? Porque tenes un 1/2 de la ecuación y otro que sale de multiplicar por la velocidad angular.
Hola Sebastián,
el eje vertical (llamémosle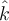 
a la vertical) que pasa por 
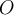es el eje instantáneo de rotación de la pieza, por lo que la energía cinética de la misma es: 
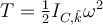, siendo 
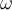la velocidad angular de rotación alrededor del eje; no alcanzo a entender el factor 
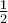extra que sería esperable (ojo porque el momento de inercia 
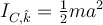, quizás de ahí te pueda surgir la duda, pero el 1/4 recién aparecería al desarrollar la forma general de la energía cinética).
Saludos,
Ariel.
Hola, en la parte 2.b de la solución se plantea que el cuadrado de x(punto) debe ser menor que cero, para que la masa no alcance el extremo A. Pero, como puede ser que el cuadrado de una cantidad sea negativa? No tendría que igualarse a cero? Gracias
Hola,
Justamente, el punto es que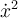 
jamas puede ser negativa, por lo que, de serlo, esto de hecho quiere decir que la particula jamas va a estar ahi, que es precisamente lo que se quiere imponer.
Es decir, en este ejercicio, combinando la conservacion de la energia del sistema barras + particula y la conservacion de la componente vertical del momento angular del mismo sistema, se llega a una ecuacion de la forma
donde adentro de la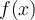 
tambien hay dependencia en las condiciones iniciales. El punto es que la particula solo puede estar en las regiones de 
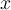para las cuales 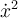es mayor a 0. Si queremos que la particula no llegue a 
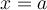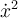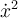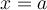, lo que debemos imponer es que este punto este fuera de la region permitida para la particula. Fuera de la region permitida para la particula es menor a cero, por lo que queremos es que en sea menor que cero.
El caso en que 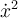es igual a cero en 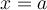seria el caso limite en que 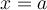corresponde justo a la frontera entre la region permitida y la no permitida. En este caso la particula llegaria "justito" a .
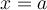Espero que esto responda a tu pregunta
cualquier cosa no dudes en repreguntar
saludos
g
Se entiende perfecto, graciass
Buenas, en la parte b, en la solución, al calcular el momento de inercia desde el punto C, toma el de la parte A, pero no habría que agregarle el momento de inercia de la masa puntual?
En la parte b) básicamente hay que usar conservación de la energía y la componente vertical del momento angular del sistema completo: Marco cuadrado + partícula.
La expresión para la energía cinética que dieron más arriba es válida para un rígido, pero la partícula no está incrustada al marco, se puede mover sobre uno de sus extremos por lo que el sistema marco + partícula no es un rígido. Para hallar estas cantidades hay que hallar las correspondientes al marco, luego a la partícula y después sumarlos. Si una partícula está en reposo con respecto a un rígido entonces sí se puede considerar parte del mismo y se puede hacer lo que vos decís.
Saludos