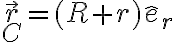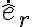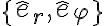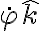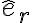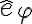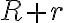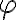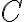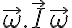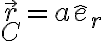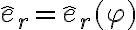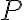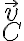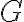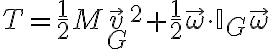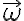ej 9

ej 9

de Ignacio Zana Rodriguez -
Número de respuestas: 4

Buenas, tengo una duda sobre la velocidad del punto C que aparece en las soluciones. Yo intente hallarla a partir de la posición del pto C, pero me queda bastante distinta a como está en la solucion.

La posición de C depende de (R+r) segun êr y de la coordenada phi según êphi. Si yo derivo esta expresión para hallar la vel. de C, me  queda según los versores  êr y  êphi; pero en la solución subida solo depende de êphi.

A la hora de derivar, yo utilicé como velocidad angular del sistema 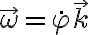  \vec{ \omega } =\dot{ \varphi }\vec{k}

Pero me surge la duda si es esa la vel. angular que debo usar o la del disco, que seria 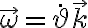  \vec{ \omega } =\dot{ \vartheta }\vec{k}

De todas maneras, utilizando cualquiera de las dos vel. angulares, nunca llego al resultado de las soluciones.
En respuesta a Ignacio Zana Rodriguez

Re: ej 9

de Ariel Fernández -

Estimado Ignacio,

a partir de la posición del punto C desde el centro del disco fijo:

\vec r_C=(R+r)\hat e_r,

podés derivar en el tiempo y hallar la velocidad de este punto (se trata de un punto del rígido de identidad material definida, por lo que seguirlo y derivar es correcto).

Luego, para hallar \dot {\hat e}_r podés usar que la velocidad angular de la base \{\hat e_r, \hat e_{\varphi}\} es \dot {\varphi}\hat k y considerar el producto vectorial de esta velocidad angular con \hat e_r (estás derivando versores de una base dada por lo que la velocidad angular que interviene es la de la base misma, no tiene relación con la velocidad angular del rígido), por lo que llegás a que la velocidad del punto C es según \hat e_{\varphi}

(Observá además que el punto C recorre una circunferencia [de radio R+r], por lo que su velocidad debe ser tangente a esa circunferencia, es decir, según \hat e_{\varphi}).

Saludos,

Ariel.
En respuesta a Ariel Fernández

Re: ej 9

de Ignacio Zana Rodriguez -

Gracias Ariel por la respuesta.

Por qué la posición del punto C no está también determinada por el ángulo  \varphi ? Para uno dar la posición del centro del disco chico, no tiene que dar la distancia al centro del disco grande más el ángulo que forma con la vertical que pasa por el pto O?

Y otra duda, estoy intentando hacer la parte a) con la energía, y me estoy tomando como punto de referencia el punto  C ; cómo me quedaría el término  \vec{ \omega }.\vec{I}\vec{ \omega } ?  Yo me estoy tomando el tensor de inercia para un disco plano, y \vec{ \omega } =\dot{ \vartheta }\vec{k}  como velocidad angular. Pero el resultado que llego no es el correcto, no me doy cuenta en que le estoy fallando.

Saludos
En respuesta a Ignacio Zana Rodriguez

Re: ej 9

de Ariel Fernández -

Hola Ignacio,

el ángulo \varphi influye sí en la posición de C (de hecho es la coordenada con la que ubicás al punto sobre la circunferencia en la que se mueve), es que al escribir \vec r_C=a\hat e_r el versor \hat e_r tiene dependencia en \varphi: \hat e_r=\hat e_r(\varphi) (te recomiendo ver en los Apuntes 2010 el comentario que sigue a la ec. (1.6)).

En cuanto a la energía cinética, al tomar como referencia el punto C, a diferencia de P que tiene velocidad nula, debés tomar en cuenta \vec v_C para el cálculo, que por ser C el centro de masas G del disco, te queda de esta forma (ec. (7.35)):

T=\frac{1}{2}M\vec{v}_G\hspace{1mm}^2+\frac{1}{2}\vec{\omega}\cdot\mathbb{I}_G\vec{\omega}

donde \vec\omega es como bien estás usando, la velocidad angular del rígido (Nota: la energía cinética es una cantidad escalar que no tiene punto de referencia, tomamos alguno que nos resulte conveniente para el cálculo pero nada más, así que con la forma correcta los resultados deberían ser coincidentes).

Saludos,

Ariel.