El disco grande no está en movimiento. Es simplemente un vínculo para el movimiento del disco chico. Por lo tanto te conviene aplicar las cardinales solo al disco chico. No se conoce el sistema de fuerzas que mantiene fijo el disco grande.
Si vas a aplicar la segunda cardinal al disco chico en el centro del disco grande tenés que tener en cuenta que ese punto, considerado como punto del disco chico, no está fijo. Además vas a tener que tener en cuenta el momento de la fuerza de rozamiento en el punto de contacto.
Creo que es más fácil aplicar la segunda cardinal en el punto de contacto´(para que no te aparezca ese momento).
O también en el centro de masa del disco chico. En este caso te aparece el momento de esa fuerza por lo que vas a tener que aplicar la primera cardinal. Y no es problema, porque esa fuerza la vas a precisar para estudiar la rodadura sin deslizamiento.
Además podés estudiar si mientras tenés rodadura sin deslizamiento, el sistema no es conservativo. Si lo es, podés usar el teorema de la energía para hallar la ecuación de movimiento. O mejor aún, como dice la sugerencia, para verificar lo que obtengas por cardinales.
Muchas gracias. Me surgió otra duda al aplicar la cardinal sobre el centro de masa del disco chico
Cuando escribo w tengo que tener en cuenta solo el giro que tiene el disco chico sobre el eje que pasa por su centro de masa y es perpendicular al disco, o también tengo que sumarle a esta expresión la velocidad angular con respecto al centro del disco grande (ro punto)? Porque por ambos caminos llego al resultado correcto, pero supongo que alguno es incorrecto.
La velocidad angular del disco chico es una sola. Podés llamarle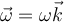 
, donde 
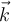es un versor saliente del plano de la figura. Como vimos en movimiento relativo esta velocidad angular va a estar vinculada a cómo se mueven los versores solidarios al disco respecto a un sistema de referencia fijo.
Mientras el disco rueda sin deslizar esta velocidad angular va a estar relacionada con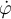 
por una relación que se obtiene de aplicar la distribución de velocidades para que el punto de contacto tenga velocidad cero. Esto debe tener en cuenta que la velocidad del centro del disco está dada por 
.
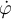Cuando el disco desliza ya no se cumplirá esa relación y ω ya no va a estar vinculada con .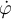
Hola,
mirando la solución que subieron de este ejercicio, no entiendo cuando usa distribución de velocidades para calcular la del punto C, la toma respecto a P (usa el radio r=a/4) en vez de con respecto a O que sería el sistema fijo y ahí el radio R+r quedaría a.
Gracias
La distribución de velocidades se usa entre dos puntos del rígido. El punto O no es un punto del disco exterior (si tomo cualquier punto del mismo que no sea su centro, la distancia del mismo a O no es constante). Se podría tomar cualquier punto del rígido pero el más conveniente es O por tener velocidad cero (el disco exterior rueda sin deslizar sobre el disco más grande, que está quieto).
Buenas, yo quise aplicar la segunda cardinal en el punto de contacto P, como lo menciona Ricardo, pero no pude llegar a la ecuación correcta final, presiento que mi error es cuando escribo la aceleración en P, ¿cómo les queda?
Mi segunda cardinal aplicada en P me queda de la siguiente manera:
m(P-C)×aP + Ip,k. (dw/dt) = (mga/4).senφ
Saludos
Estimado Nicolás,
en tu planteo de la Segunda Cardinal tenés que cambiar el signo del primer término (debería decir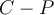 
ya que 
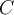es el CM del disco) y necesitás hallar la aceleración instantánea de 
: 
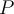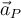, la cual podés vincular con la de 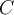(conocida fácilmente porque se trata de un punto de identidad material) a partir de la distribución de aceleraciones en un rígido (ec. 6.3 apuntes 2010). Podés ver luego que 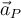es colineal con 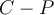, por lo que el primer término del lado izquierdo de la Segunda Cardinal es nulo.
Saludos,
Ariel.
Muchas gracias por tu respuesta, quedó claro. Saludos