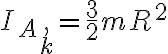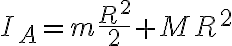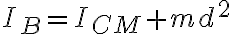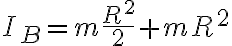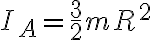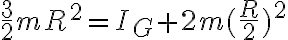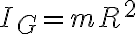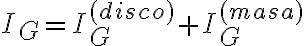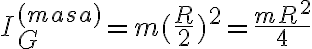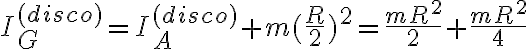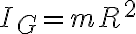Ejercicio 6

Ejercicio 6

de Leandro Jair Machado Da Silva -
Número de respuestas: 7

Hola, intento hallar la ecuación de movimiento del sistema por energía pero me surge la siguiente duda: cómo afecta el tener una partícula incrustada al disco al tensor de inercia? o, más bien, al momento de inercia con respecto al eje perpendicular al plano del movimiento (ya que es lo que me interesa, pues 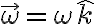 \vec{\omega}=\omega\hat{k} ). Puede ser que como es una partícula y no un cuerpo de masa continuo no afecte en nada? Me surge esta duda al intentar calcular al energía cinética, gracias.
En respuesta a Leandro Jair Machado Da Silva

Re: Ejercicio 6

de Ariel Fernández -

Hola Leandro,

el tensor de inercia (es decir cualquiera de sus elementos, como el momento de inercia que necesitás para este problema plano) es aditivo en la masa del sistema. Para el caso de este problema podés calcular el momento de inercia del disco según el eje 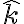\hat k pasando por un cierto punto (el centro del disco si querés) y sumarle el momento de inercia de la masa 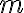m para el mismo eje y el mismo punto (la masa cuenta sí, se trata de un punto con una masa concentrada en él y finita).

Te recomiendo que veas la clase por la plataforma Zoom  del viernes pasado que trató sobre este ejercicio:

https://drive.google.com/drive/folders/1iLzpy-8Po5uD409Ce4CCJ93T9eeWRpRR?usp=sharing

y para ver una caso más de cómo se considera la contribución aditiva de masas puntuales, podés ver el ejemplo de masas coplanares del final de la sección 7.1 de los Apuntes 2010.

Saludos,

Ariel.
En respuesta a Ariel Fernández

Re: Ejercicio 6

de Nahuel Borsil Pastorino -
Hola, tengo una confusión con esto mismo que hablan.

Si entendí bien para calcular el momento de inercia por A según k puedo usar que este es aditivo de las masas, eso también lo vi por esta ecuación. 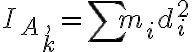 I_A,_k= \sum{m_id_i^2} .

Usando esta ecuación lo que hice fue sumarle al momento de inercia del disco sin la partícula incrustada (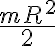 \frac{mR^2}{2} ) un elemento más a la sumatoria que sería  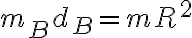m_Bd_B=mR^2 correspondiente a la partícula B lo que me daría:

I_A,_k= \frac{3}{2}mR^2

Pero al ver la clase de este ejercicio parece que este momento de inercia es respecto a B y no a A como me dio a mí, ademas comentan que usan Steiner de manera que 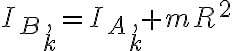 I_B,_k=I_A,_k+ mR^2 y toman  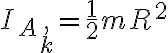I_A,_k= \frac{1}{2} mR^2 que es el momento del disco como si no tuviera una partícula incrustada y esto es lo que no entiendo, para hacer esa cuenta como en la clase de zoom no se necesita el momento de inercia respecto a A del disco con la partícula? es el momento de inercia respecto a A del disco el mismo que el del disco con la partícula?

En la clase además dicen que el punto B no tiene inercia por ser una masa puntual, pero en el mensaje de aquí arriba dice que la masa B si cuenta para el momento de inercia, como es esto?

Saludos
En respuesta a Nahuel Borsil Pastorino

Re: Ejercicio 6

de Guzman Hernandez -

Hola,

Hay algo aca que confunde un poco las cosas y es que la masa puntual y el disco tienen la misma masa. A los efectos de explicar que es lo que esta sucediendo voy a suponer que la masa incrustada tiene masa 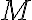M y el disco tiene masa m .

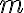El razonamiento que vos haces sobre la aditividad del momento de inercia en la masa esta bien. En estos terminos, el momento de inercia de todo el rigido con respecto a A queda

I_{A} = m\frac{R^2}{2} + MR^2

donde el primer termino es el momento de inercia del disco con respecto a A (que es el centro de masa  del disco) y el segundo termino es la contribucion de la masa incrustada al momento de inercia en A. El razonamiento es exactamente el que vos hiciste.

Ahora vamos a calcular el momento de inercia con respecto a B. La masa puntual no contribuye al momento de inercia con respecto a B por que esta en B. Tiene "distancia cero" con respecto a ese punto. Entonces en el momento de inercia con respecto a B es el momento del disco con respecto a B. para calcularlo usamos el teo de los ejes paralelos

I_B = I_{CM} + md^2

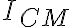donde I_{CM} es el momento de inercia del disco con respecto al centro de masa y 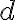d es la distancia del centro de masa a B. Nota que aca no aparece la masa incrustada en absoluto, esto es el teor de los ejes paralelos PARA EL DISCO. Como dijimos, el centro de masa del disco esta en A, asi que 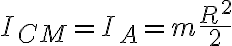I_{CM} = I_A = m\frac{R^2}{2} y la distancia entre el cm del disco y B es 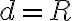d = R . Juntando todo tenemos la formula de la clase de practico

I_B = m\frac{R^2}{2} + mR^2

espero que esto aclare tu duda

cualquier cosa no dudes en repreguntar

g
En respuesta a Guzman Hernandez

Re: Ejercicio 6

de Nahuel Borsil Pastorino -

Si, ahora queda claro. Una pregunta más, dado que efectivamente el momento de inercia en A es  I_A= \frac{3}{2}mR^2 es posible calcular el momento por el centro de masas usando Steiner?... \frac{3}{2}mR^2=I_G+2m (\frac{R}{2})^2

En ese caso  I_G=mR^2  

Mi duda va en que quizás no se pueda porque la distribución de masa no es homogénea

Saludos
En respuesta a Nahuel Borsil Pastorino

Re: Ejercicio 6

de Ricardo Marotti -


Ese resultado es correcto. El teorema de Steiner vale siempre, para figuras homogéneas y también para las que no lo son. 

Podemos verificar ese resultado por otro camino. Si G es el centro de masa del sistema total (el punto medio entre A y B); 

I_G = I_G^{(disco)}+I_G^{(masa)}

Luego: 

I_G^{(masa)} = m( \frac{R}{2})^2 = \frac{mR^2}{4}

Y aplicando Steiner solo para el disco (donde A es su centro de masa): 

I_G^{(disco)} = I_A^{(disco)} + m( \frac{R}{2})^2= \frac{mR^2}{2} + \frac{mR^2}{4}

Y sumando todo me da: 

I_G=mR^2