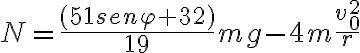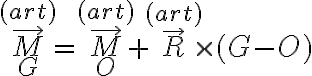No entiendo como hacer esta parte del ejercicio. Queria ver si me podian dar alguna idea de como hacerlo.
Hola Juan, buen día.
Podés empezar por ver la reducción de un sistema de fuerzas sobre un rígido, por ejemplo en los Apuntes 2010 sección 8.2.2.
En el caso de este problema tenés que notar que alrededor del punto 
hay un sistema de fuerzas aplicadas radialmente ya que el contacto es liso, por lo que el momento del sistema de fuerzas visto desde 
se encuentra directamente.
Para ver la resultante del sistema de fuerzas vas a necesitar aplicar la primera cardinal a la barra y usar la información de la parte a), de donde vas a poder sacar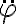 
y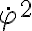 
que intervienen en la aceleración del centro de masas.
Finalmente, para averiguar el momento del sistema de fuerzas visto desde , podés usar la fórmula de cambio de punto de aplicación de momentos (sección 5.3.1) y relacionar ese momento con el visto desde , que ya averiguaste antes.
Suerte y cualquier cosa volvé a preguntar nomás.
Saludos,
Ariel.
Hola. Yo no entiendo como encontrar T. Ademas intente llegar a N por la energía y llego a un valor muy parecido, pero en el primer termino en vez de tener un 3 tengo un 27.
Buenas!
Tanto N como T son producto del vínculo entre la barra y la circunferencia, la idea es que asumas que efectivamente hay una normal y una fuerza tangencial y al plantear la 1a cardinal las despejes en base a las fuerzas que ya conocés (el peso) y las expresiones de las derivadas de phi que aparecen en la aceleración del baricentro.
Respecto al valor numérico de la respuesta, es posible que haya un error en la solución si, yo en vez de un 3/19 tengo un 51/19...
Espero que te sirva!
Estimado Sebastián,
el resultado va tal como te adelantaba Tomás, te dejo por aquí lo de da la reacción normal:
(el práctico está ahora corregido con el resultado correcto).
Saludos,
Ariel.
Buenas
Me sumo a las dudas de este ejercicio. Pude llegar a los resultados pero no entiendo a que se debe la componente tangencial si el contacto es liso. Agradezco si me pudieran aclarar eso
Lo diferente del contacto de este ejercicio es que se trata de un contacto distribuido. Es decir no es un contacto puntual. Como tal no tiene definida una única componente tangencial. Sino que cada elemento diferencial del contacto es liso, y son estos contacto infinitesimales que no tienen componente tangencial. Pero sí hay componente normal, que cambia su dirección para cada elemento diferencial. Esto hace que la resultante de fuerzas tenga una componente según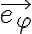 
.
Buenas,
No llego a la ecuación de movimiento correcta y no me doy cuenta cual es mi error
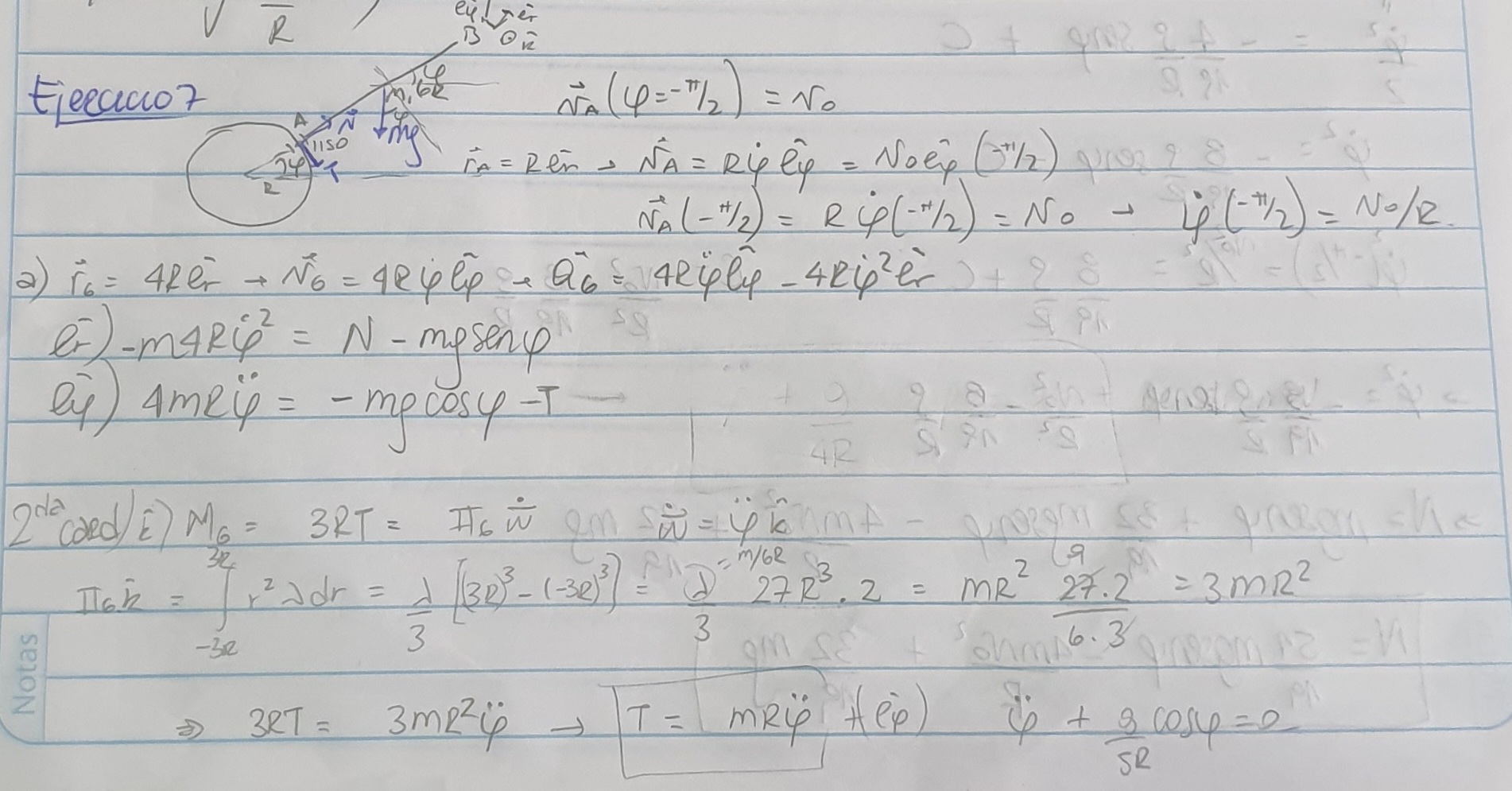
Hola Manuela,
el único problema que encuentro en tu planteo es que al considerar la 2da Cardinal estás tomando como que el contacto en la articulación es puntual cuando en realidad es distribuido (ver el mensaje de Ricardo más arriba): el sistema de fuerzas actuando en la articulación se puede reducir a una resultante actuando en un punto (si tomamos que ese punto de referencia es coincide con tu diagrama de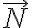 
y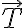 
actuando en ) más un momento (la parte que te falta considerar: 
).
Para tratar la Segunda Cardinal desde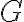 
deberías trasladar el momento desde usando la fórmula de cambio de punto de aplicación de momentos (ec. (5.13) Apuntes 2010):
(el segundo término del lado derecho es lo que tenés vos planteado, que corresponde a la resultante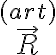 
del sistema de fuerzas en la articulación actuando en ).
Sólo te faltaría arreglar tu segunda cardinal, para lo cual podés usar la fórmula de cambio de momentos pero vinculando 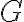con :
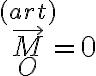(más sobre ésto en la respuesta al siguiente mensaje); luego la forma en que combinás tu segunda cardinal con la componente tangencial de la primera te permite eliminar 
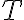y hallar la ecuación de movimiento.Alternativas para explorar y verificar que se llega a lo mismo:
i) Usar sólo la segunda cardinal pero directamente desde (ya que 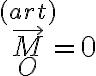y vas a tener involucrado sólo al peso)
ii) Usar que se conserva la energía
Saludos,
Ariel.
Buenas, no me queda claro cómo tomar un sistema de fuerzas aplicadas con respecto a A pero luego tomar el momento con respecto O. Si tomo el sistema con respecto a A, eso no me dice que el momento de las fuerzas externas con respecto a A es 0? En dónde entra O ahí? (Todo esto me refiero con respecto al mensaje que puso Ariel al principio del hilo)
Muchas gracias!!
Hola Francisco,
para aclarar un poco el panorama con respecto a este ejercicio veamos un poco más en detalle qué pasa dentro de la articulación (ver adjunto).
El sistema de fuerzas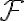 
actuando sobre la articulación lisa alrededor de es distribuido: tenemos un conjunto de puntos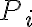 
cercanos a (que podemos marcar por una posición angular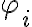 
cercana a 
) en los cuales la guía ejerce sobre la articulación una fuerza que sólo tiene componente normal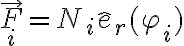 
. Como la guía es circular, la dirección normal a la misma es radial, por lo que el momento desde de cada fuerza 
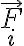del sistema es nulo y por lo tanto, la suma de ellos también: 
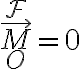(o para compatibilizar con mensajes anteriores ).
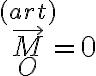Si tomamos como referencia , la dirección radial de cada fuerza no implica que el momento del sistema desde este punto sea nulo. Lo que puede resultar un poco confuso en las articulaciones en general es considerar a priori que como las fuerzas se aplican muy cerca del punto de interés, su momento va a ser nulo. No hay que olvidar que tratamos con un conjunto de fuerzas que se aproxima al continuo, por lo que aún cuando individualmente no parezcan aportar nada significativo, en la suma sí lo pueden hacer.
De hecho, al aplicar la fórmula de cambio de momentos entre y , habiendo hallado la resultante previamente, podés ver que 
.
Saludos y cualquier otra duda a las órdenes.
Ariel.
Clarísimo! Muchas gracias
Muchas gracias! Me quedó una duda igual. Si tomamos como que mi sistema de fuerzas aplicado en A, consiste solo de fuerzas Normales Ni, entonces por qué después tengo que considerar una componente tangencial? Porque al agregar esa T, el momento de las fuerzas de O, ya no sería 0 no?
En respuesta a Francisco Jose Garchitorena Topolanski
Re: Ejercicio 7, parte b
de Guzman Hernandez -
Hola
Fijate que esas fuerzas Ni que mencionas tienen todas distinto punto de aplicaci;on, asi que si bien son todas radiales, apuntan en distintas direcciones. Genericamente, la resultante (es decir la suma) de todas estas fuerzas radiales pero que apuntan en distintas direcciones va a ser un vector arbitrario en el plano. Es decir que si ahora tomo una base de vectores en el plano dado por una direccion radial especifica (la direccion radial en A) y su tangencial correspondiente, dicha resultante va a tener componente en las dos direcciones. Eso no quita que el momento con respecto a O de este sistema de fuerzas sea nulo, ya que todas las fuerzas Ni son radiales.
Creo que tu confusion es en la descomposicion de un sistema de fuerzas en una resultante y un momento con respecto a un punto, El error es que el momento con respecto a O NO ES el momento de la resultante con respecto a O como si estuviera aplicada en A,
espero que esto te haya aclarado
en cualquier caso no dues en repreguntar
saluds
g
Hola, no sé si mi razonamiento está bien después de leer las respuestas de esta parte del ejercicio 7.
En realidad, no hay fuerza tangencial de la articulación porque esta es lisa, hay una radial por lo que el momento de esta fuerza desde O es cero.
La fuerza tangencial aparece porque como te pide el momento de la articulación desde A usas la reducción del sistema de fuerzas a un par y a una resultante que descompones en una tangencial y una normal, ¿de ahí T?
Gracias!!
La idea es que es un contacto distribuido: hay muchos puntos que están en contacto. Para cada punto hay una dirección radial, que cambia de punto en punto; así como cambia la dirección tangencial. La resultante es la suma de todas las componentes radiales, que a priori va a tener dos componentes: una según la dirección de la barra y otra perpendicular a esta. No hay razón para decir que la resultante según la dirección perpendicular a la barra sea cero (porque las normales aplicadas en cada punto cambian su dirección y dan una resultante no nula según esa dirección).
Obviamente que también hay un par aplicado que es lo que genera el momento no nulo en A. Ahora, como este momento en O es cero, el par en A va a tener que ser -rT, para compensar el momento en O de la resultante según la dirección perpendicular a la barra (al aplicar la fórmula de cambio de momentos entre O y A).