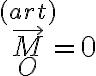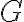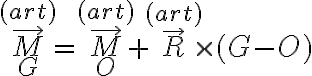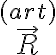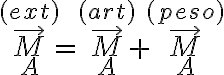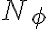Hola
Quiero poder hallar la ecuación de movimiento sin recurrir a energía y para ello necesito plantear la 2da cardinal de manera que me aporte información sobre las fuerzas reactivas. Intenté hacerlo desde el CM planteando una fuerza reactiva general pero no llego al mismo resultado. Como podría plantearlo correctamente?
Muchas gracias
Estimado Lorenzo,
podés llegar a la ecuación de movimiento planteando la segunda cardinal a la barra desde el punto 
ya que el momento del sistema de fuerzas sobre la articulación es nulo visto desde ese punto (
). En este planteo sólo te va a aparecer momento del peso y alcanzás la ecuación de movimiento sin involucrar a las reactivas.
Te recomiendo revisar el hilo correspondiente a la pregunta de la parte b de este Ejercicio para ver algún detalle de y una buena discusión de temas relacionados.
Saludos,
Ariel.
Muchas gracias!
Buenas, yo quise hacer esta parte utilizando el momento de fuerzas en el CM y aplique lo que tu, Ariel, sugeriste en el foro. Adjunto mi planteo en una foto de la 2da cardinal. La primera cardinal me quedo de la siguiente manera:
4mr. d2φ / (dt)2 = - mgcosφ + Nφ
donde Nφ es la reacción tangencial en la articulación A que la obtuve de aplicar la 2da cardinal para luego sustituirla en la 1ra cardinal y así obtener la ecuación de movimiento.
Mi temor es que este realizando un error de razonamiento, por eso decidí poner todas las cuentas por si acaso. Muchas gracias
Estimado Nicolás,
Tu primera cardinal en la dirección tangencial está bien, pero al trasladar el momento de a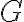 
:
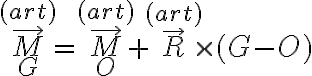
no estás considerando bien la componente tangencial de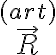 
(al despejar de la primera cardinal te falta el término en 
).
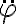Luego, en el planteo de la segunda cardinal desde 
te falta considerar el momento de todas las fuerzas, no sólo la articulación:
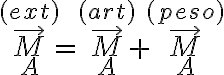
y te está faltando entonces el momento del peso.
Tal como le sugería a quien preguntó en el mensaje al que creo que te estás refiriendo y en un mensaje original sobre este ejercicio, a efectos de la ecuación de movimiento intentaría alternativas que no involucren a las reactivas:
i)
Usar sólo la segunda cardinal pero directamente desde (ya que
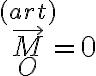y vas a tener involucrado sólo al peso)
ii) Usar que se conserva la energía
Los anteriores son planteos más directos para llegar a la ecuación de movimiento, con la que luego podés encontrar la resultante de las fuerzas en la articulación y su momento visto desde (no hay nada malo en tomar de arranque una segunda cardinal desde o 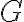y combinar con la información que sale de la primera y la fórmula de cambio de momentos, es sólo a efectos de poder despejar la ecuación de movimiento más directamente y dejar las reactivas para el final).
Saludos,
Ariel.
Muchas gracias por tu respuesta Ariel, me queda dos dudas al respecto, ¿cual es tu argumento para demostrar que el momento de fuerzas en O de la articulación es nula si debido al contacto de distribución aparece una normal tangencial que llamé Nφ en A?
Y la segunda duda es, Nφ debe ser contrario al crecimiento de φ, a que se debe esto? Pregunto pues si yo hubiera elegido un sentido contrario para Nφ me da un resultado diferente.
Nuevamente agradezco tu tiempo, saludos
Hola Nicolas,
para ver que el momento de las fuerzas sobre la articulación con respecto a es nulo, te recomiendo ver los mensajes bajo Ejercicio 7 parte b en este mismo Foro, donde discutimos bastante en detalle ese punto y cómo no entra en contradicción con tener una componente tangencial de la resultante del sistema (las fuerzas del sistema ejercido por la guía circular sobre la articulación son radiales, es decir, tienen recta de acción que pasa por , pero su suma puede tener [y tiene] componente tangencial con respecto a una posición angular dada [la que ubica a ]).
Con respecto a tu otra duda, no sé si alcanzo a entender cómo el resultado para la reacción tangencial entra en contradicción con alguna intuición que tengas con respecto a esta reactiva, si querés mandá otro mensaje un poco más detallado por favor; en principio es una fuerza que "se acomoda" al movimiento de la barra, movimiento que uno puede obtener a partir de la conservación de la energía o segunda cardinal desde , donde no está implicada ninguna reactiva. Luego, las componentes tangencial y normal son tales que el movimiento que podemos analizar a partir de la primera cardinal sea el mismo que el obtenido previamente.
Saludos,
Ariel.
Hola Ariel, agradezco tu respuesta, ya había visto los mensajes en el foro explicando mi primer duda pero lamentablemente no había terminado de entender, por esa razón quise preguntar nuevamente.
Respecto a lo de la normal, mi primera cardinal respecto a eφ quedó:
4mr. d2φ / (dt)2 = - mgcosφ - Nφ (1)
Si yo decido plantear la 2da cardinal con respecto al CM me aparece Nφ y de aquí despejo Nφ para insertarlo en mi ecuación (1). Aquí es cuando afirmo de la relevancia del sentido de la componente tangencial Nφ pues si elijo poner Nφ en sentido contrario llego a una diferente ecuación de movimiento. Saludos
El sentido de 
lo podes poner para cualquier lado, mientras seas consistente en las dos cardinales. Si hubieras puesto para el otro lado en la 1ra card tambien tenias que cambiar el sentido en la segunda (el torque de la fuerza cambia de signo si la fuerza es para el otro lado) por lo que los sistemas de ecuaciones en un caso y en otro son equivalentes.
Dijate que si despejas de una la 2da card en el CM y lo enchufas en la ec de la 1era card, llegas a una ec de mov que es la misma que obtendrias si plantearas directamente la segunda cardinal en O. En verificar que los dos son equivalentes juega crucialmente el teorema de los ejes paralelos para trasladar momentos de inercia.
Espero que esto responda tu pregunta
si no fui claro no dudes en repreguntar
saludos
g
Uhh si, pequeño detalle me comi! Muchas gracias, saludos