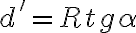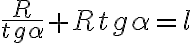De la figura que hizo Esteban se puede ver que el lado del rombo (que vale l, la longitud de una barra) es la suma de dos distancias (llamémosle d y d´) que son catetos de triángulos rectángulos que tienen ángulos α, y el otro cateto vale R. Uno de ellos es cateto adyacente al α dibujado por Esteban (llamésmole d), del que R es cateto opuesto, entonces:
El otro es cateto opuesto (llamémosle d´). Aquí hay que ver que el ángulo opuesto a este cateto es α porque las rectas que lo forman son perpendiculares a las del ángulo α dibujado por Esteban. Y R es cateto adyacente a este ángulo α, entonces:
Luego:
El resto es escribir tg α en función de sen α y cos α y operar.