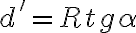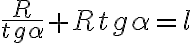No entiendo como llegar al segundo angulo(angulo máximo) de la solución, agradezco cualquier sugerencia o guía.
El segundo ángulo corresponde a una condición geométrica del problema, que es cuando el disco toca las dos barras de arriba. Si el otro resultado es menor que ese ángulo, no es una situación posible, y la condición de equilibrio es cuando el disco queda apretado por las cuatro barras.
Entiendo que ahora sea este el caso pero no entiendo que cuentas realizar, ya que el potencial no cambia.
Sebastián, que tal?
Recién veo tu mensaje, perdón por la tardanza!
Lo que te dice Ricardo, es que para el segundo ángulo, en realidad no hay que usar la energía, es una condición geométrica de lo que pasaría si, dadas las dimensiones del disco y las barras, el disco queda en contacto con las 4 barras.
En ese caso podés encontrar relaciones que te llevan al ángulo de la respuesta.
Te aconsejo buscar relaciones para los rombos (las 4 barras van a formar un rombo), para llegar a la respuesta correcta.
Cualquier cosa preguntá de nuevo.
Suerte!
Hola! No entiendo por qué la respuesta final es el máximo de los dos ángulos que se hallan. Por otro lado, no entiendo tampoco cómo darme cuenta de que ese último ángulo del cual están hablando, es también una posición de equilibrio. Estamos hablando de que el disco esté circunscripto al cuadrilátero, verdad? Por qué esto significa que el sistema va a estar en equilibrio (si es que este ángulo es mayor al anterior, cosa que tampoco entiendo la razón)?
Leandro, la idea es que una vez que se alcanza el segundo ángulo, el sistema queda trancado. Por lo tanto el ángulo que minimiza el potencial, si es menor a este último, no se alcanza. Sin embargo si el ángulo que minimiza el potencial es mayor a este ángulo, si lo alcanza. Está más claro?
Para ver como encontrar el segundo ángulo te aconsejo lo mismo que le dije a Sebastián, tenés que ver como queda el ángulo en función de R y l para el caso en el que el disco queda efectivamente circunscripto.
Suerte!
Hola, no estoy pudiendo llegar al ángulo en el caso en que el disco queda circunscripto al rombo, alguna ayuda? gracias
A ese ángulo se llega por geometría únicamente. Se impone que el disco quede circunscripto en el rombo.Para obtener la solución se podría hacer algo así: Dibujá el rombo y el disco circunscripto en el mismo:
La distancia del centro hacia el punto superior del rombo se puede escribir en función de l y alpha, y se puede escribir también de otra forma en función de R y alpha.
Igualando esas dos expresiones y usando la relación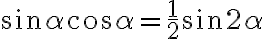 
se llega al resultado.
Hola, no estaria llegando a la solucion usando esa relacion, ademas cuando igualo las distancias del centro al punto superior me queda dividiendo el seno entre el coseno y no me serviria la relacion dada
De la figura que hizo Esteban se puede ver que el lado del rombo (que vale l, la longitud de una barra) es la suma de dos distancias (llamémosle d y d´) que son catetos de triángulos rectángulos que tienen ángulos α, y el otro cateto vale R. Uno de ellos es cateto adyacente al α dibujado por Esteban (llamésmole d), del que R es cateto opuesto, entonces:
El otro es cateto opuesto (llamémosle d´). Aquí hay que ver que el ángulo opuesto a este cateto es α porque las rectas que lo forman son perpendiculares a las del ángulo α dibujado por Esteban. Y R es cateto adyacente a este ángulo α, entonces:
Luego:
El resto es escribir tg α en función de sen α y cos α y operar.