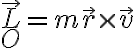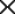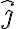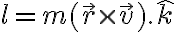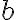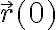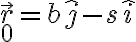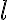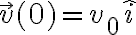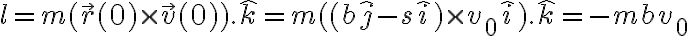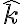Hola,
Lo que se conserva en el movimiento central es el momento angular con respecto al origen de la fuerza central. Esta cantidad se define como
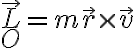
Antes de seguir adelante, te comento que el s'imbolo 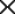 se reserva para el producto vectorial. En tus f'ormulas lo usas para el producto entre n'umeros que en general no lleva simbolo. Ese uso es bastante confuso.
se reserva para el producto vectorial. En tus f'ormulas lo usas para el producto entre n'umeros que en general no lleva simbolo. Ese uso es bastante confuso.
La preintegral del movimiento a la cual referis es la componente del momento angular en la direccion perpendicular al plano en el que transcurre el movimiento. Digamos que en este ejercicio el movimiento transcurre en el plano definido por los versores  y
y 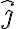 . Entonces la cantidad conservada se define como
. Entonces la cantidad conservada se define como
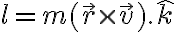
Calculemos el valor de esta cantidad en el instante inicial del movimiento. Inicialmente la part'cula viene desde el infinito con un par'ametro de impacto 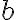 . Podemos pensar eso de la siguiente manera. Podemos escribir la posicion inicial
. Podemos pensar eso de la siguiente manera. Podemos escribir la posicion inicial 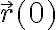 de la siguiente manera
de la siguiente manera
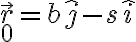
y usar esta expresi'on para calcular el momento angular, eventualmente tomando el limite en que  tiende a infinito, dado que la particula viene desde el infinito.
tiende a infinito, dado que la particula viene desde el infinito.
Notar que 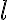 es una cantidad conservada, por lo que podemos calcular su valor en el instante inicial y este se va a mantener en todo el movimiento.
es una cantidad conservada, por lo que podemos calcular su valor en el instante inicial y este se va a mantener en todo el movimiento.
Si la velocidad inicial de la partícula la escribimos como
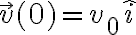
entonces tenemos
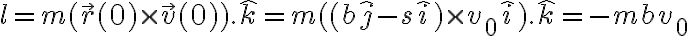
que es el resultado de la soulci'on, a menos de un signo que es convencional (nosotros tomamos 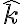 para arriba) y que no afecta el resto del problema por que
para arriba) y que no afecta el resto del problema por que 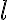 aparece siempre elevado al cuadrado. Nota que
aparece siempre elevado al cuadrado. Nota que  desaparecio del calculo, asi que tomar el limite
desaparecio del calculo, asi que tomar el limite  tendiendo a infinito es trivial.
tendiendo a infinito es trivial.
Espero que esto responda tu pregunta. Cualquier cosa no dudes en repreguntar
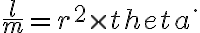 al evaluarlo en este caso me quedaría
al evaluarlo en este caso me quedaría 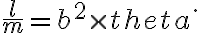 pero en las soluciones es solo b y no b a la dos. Por qué seria eso? no se utiliza la primera preintegral de movimiento central?.
pero en las soluciones es solo b y no b a la dos. Por qué seria eso? no se utiliza la primera preintegral de movimiento central?.