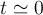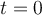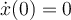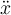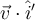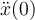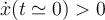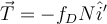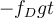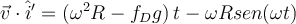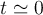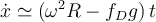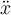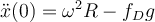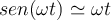MecNew: Primer Parcial 2014 Ej.1 Parte d

Buenas,

Adjunto como resolví esta parte.

Como podrán ver, si hago tender t a 0, la componente horizontal de la velocidad absoluta me da 0. No logro entender el último renglón de la solución del parcial, ¿por qué en el término que les sobrevive no hacen tender t a 0?. Si lo hicieran, llegaría a lo mismo.

Desde ya muchas gracias.

Saludos,

Pilar.

PrimerParcial2014_Ej1_Parted.pdf

Re: Primer Parcial 2014 Ej.1 Parte d

de Ariel Fernández - lunes, 25 de mayo de 2020, 14:59

Estimada Pilar,

tu solución es correcta para la componente horizontal de la velocidad cuando considerás cómo se comporta en un entorno del instante inicial: 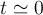$t\simeq0$ , lo que es un poco más amplio que considerar sólo qué sucede en 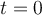$t=0$ : sabemos que el bloque parte del reposo relativo a la plataforma, por lo que la solución para 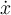$\dot x$ debe dar 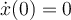$\dot x (0)=0$ , lo que te lleva luego a que la componente horizontal de la velocidad es nula en 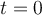$t=0$ ( esto es porque la componente horizontal de la velocidad de transporte es cero también en 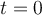$t=0$ , o dicho más fácilmente la plataforma arranca hacia arriba).

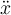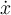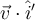En la solución está todo hecho sin aproximar primero y luego se ven las aproximaciones para un entorno del instante inicial tanto para $\ddot x$ , $\dot x$ como $\vec v \cdot \hat i'$ . En tu caso veo que calculaste bien 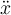$\ddot x$ pero hay un detalle en que consideraste 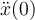$\ddot x (0)$ y luego integraste ese valor en el tiempo, lo cual funciona bien porque 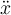$\ddot x$ se aproxima a una constante cerca del inicio y que la integración hecha así vale siempre y cuando estemos cerca del instante inicial, de lo contrario deberías integrar la expresión completa para $\ddot x$ .

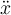Otro tema fundamental que te da el estudio en un entorno del instante inicial: para aplicar la 2da ley de Newton al bloque tuviste que suponer un sentido para la velocidad relativa a la plataforma en un entorno del instante inicial (sólo se puede suponer porque la condición inicial es de reposo relativo): suponés 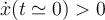$\dot x (t \simeq 0)>0$ , con lo que la fuerza de fricción dinámica te queda con sentido opuesto a esa velocidad relativa: 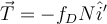$\vec T=-f_D N \hat i '$ . Una vez que se resuelve la evolución temporal, se tiene que verificar que el sentido supuesto para la velocidad relativa es tal: 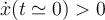$\dot x (t \simeq 0)>0$ , una suerte de test de autoconsistencia.

En definitiva: la información más interesante del problema la vas a tener haciendo una aproximación en el entorno del instante inicial, sin colapsar todo solamente a 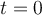$t=0$ .

Espero haberte aclarado un poco más los detalles, cualquier duda seguimos discutiendo sobre el ejercicio.

Saludos,

Ariel.

Re: Primer Parcial 2014 Ej.1 Parte d

de Pilar Martinez Menendez - lunes, 25 de mayo de 2020, 16:30

Buenas tardes Ariel,

Gracias por la respuesta.

Entiendo que al integrar directamente el resultado de la aceleración relativa en un entorno del instante inicial, estoy obteniendo un valor de la velocidad relativa que es sólo válido en ese mismo instante y no para todo t. Es decir, que si quisiera la expresión para todo t, debería integrar la expresión general de la aceleración relativa.

Lo que aún no me queda del todo claro, es por qué en un entorno del instante inicial (que entiendo no es exactamente lo mismo que t=0), la solución es: $\--f_Dgt$ y no simplemente 0. O sea, basándome en la expresión final a la que yo llegué de la componente horizontal de la velocidad absoluta. ¿Cómo debería darme cuenta que la solución se obtiene haciendo tender t a 0 en todos los términos, menos en $\--f_Dgt$ ?

Espero haber sido más clara.

Saludos,

Pilar.

Re: Primer Parcial 2014 Ej.1 Parte d

de Ariel Fernández - martes, 26 de mayo de 2020, 01:03

Hola Pilar,

considerar el entorno del instante inicial es en cierta forma quedarse a primer orden no nulo en la aproximación $t\simeq0$ ; una parte de esa aproximación ya la hiciste antes, pero analicemos la expresión de la componente horizontal de la velocidad a la que llegaste:

$\vec v \cdot \hat i'=\left(\omega^2 R-f_D g \right)t -\omega R sen (\omega t)$ .

El primer término de la anterior ya incluye una aproximación a primer orden no nulo: $\dot x$ a orden cero es nulo ( $\dot x (0)=0$ ) pero a primer orden en $t\simeq 0$ no lo es: $\dot x \simeq \left(\omega^2 R-f_D g \right)t$ , lo cual a su vez proviene de considerar $\ddot x$ a orden cero que es no nulo y vale $\ddot x (0)=\omega^2 R-f_D g$ , tal como hallaste antes.

Hagamos ahora una aproximación a primer orden sobre el segundo término de la velocidad horizontal, usando que como el argumento es pequeño, el seno se aproxima al mismo:

$sen (\omega t)\simeq \omega t$ ,

de donde nos queda:

$\vec v \cdot \hat i' \simeq \left(\omega^2 R-f_D g \right)t -\omega^2 R t=-f_D g t$

con lo que se alcanza el resultado esperado (fijate que aún cuando desde la plataforma el bloque se ve salir hacia la derecha, desde un sistema inercial sale hacia la izquierda!).

Tomar todo a orden cero te hubiera llevado a un resultado que es nulo, es necesario tomar un orden superior.

Saludos,

Ariel.