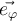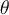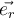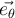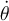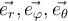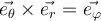MecNew: Primer Parcial 2015, Ej 2)

Buenas,

Al resolver el ejercicio respeté los sistemas de referencia que impone el ejercicio, pero haciendo esto, la velocidad angular θ(punto) me queda -θ(punto) según j´. Como la resolución no indica específicamente los sistemas de referencia que se toma, no se detectar mi error. Tal vez sea cuando planteo mi sistema móvil 2, si alguien me puede ayudar lo agradezco. Saludos ejercicio 2

Re: Primer Parcial 2015, Ej 2)

de Ricardo Marotti - miércoles, 20 de mayo de 2020, 15:19

Los errores que yo encuentro en tu solución son:

1) Está mal calculada la velocidad relativa. No lleva el signo de -. Por más que elijas la orientación de $\vec{e_ \varphi }$ como decís, cuando $\theta$ aumenta $\vec{e_r}$ se mueve según $\vec{e_\theta }$ , por lo tanto hacia allí se tiene que mover la partícula si $\dot{ \theta }$ es positivo.

Otra forma de verlo es que si yo me paro en el sistema móvil solidario a la guía, puedo trabajar en coordenadas polares con el ángulo $\theta$ . Así que si te fijás en la expresión de velocidad y aceleración de coordenadas polares, el signo de menos no va en la velocidad, y la aceleración también la tenés cambiada de signo.

2) Hay un signo mal al calcular el término $\vec{ \omega } \times (\vec{ \omega } \times \vec{r'} )$ . Ese proviene al calcular $(\vec{ \omega } \times \vec{r'} )$ te tomaste una base que no es directa. Como orientaste tus versores $\vec{e_r}, \vec{e_ \theta }, \vec{e_ \varphi }$ no es directa. La que es directa es $\vec{e_r}, \vec{e_ \varphi }, \vec{ e_\theta }$ . Básicamente $\vec{e_ \theta } \times \vec{e_r} = \vec{e_ \varphi }$ . A vos te quedó un signo de - que está mal.