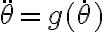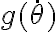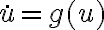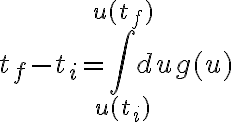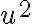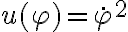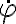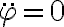Primer parcial 2017 ej 1c y 1d

Primer parcial 2017 ej 1c y 1d

de Silvina Daniela Datz Helbling -
Número de respuestas: 4

Buenas, quería consultar en el ejercicio 1c me dice que suponga que la velocidad inicial es mayor a la hallada en el item anterior, y usando esa información llego a que el fi punto inicial es mayor a la raiz de 2k/m, mi pregunta es: ¿puedo asumir que el fi punto es mayor a ese valor siempre? porque si llego a esa conclusión puedo darme cuenta en la 2da ley segun er que la normal quedaría negativa y me había equivocado al suponer que era centrífuga.

Luego, en la parte d lo que se me ocurrió era hacer un cambio de variable u=(fi punto)^2 para lograr obtener una expresión de fi punto y luego hacer el límite, no pude hacerlo porque me tranqué en las condiciones iniciales y despues vi la solución pero no la entiendo mucho

En respuesta a Silvina Daniela Datz Helbling

Re: Primer parcial 2017 ej 1c y 1d

de Guzman Hernandez -

Hola,

Si bien no podes suponer que fi punto es mayor a ese valor siempre, por un argumento de continuidad, si podes asumir que es mayor a ese valor en un entorno del instante inicial. Es correcto que en ese entorno del i nstante inicial la normal apunta para adentro. tenes que hallar la ecuacion de movimiento en ese entorno del instante inicial

con respecto a la segunda parte tenes una ecuacion de la forma


\ddot{\theta} = g(\dot{\theta})

donde g(\dot{\theta}) es una funcion de theta punto que esta dada por la ecuacion de movimiento. LLamale u a theta punto. entonces la ecuacion te queda

\dot{u} = g(u)

que la podes resolver integrando de los dos lados y te queda

t_f-t_i = \int_{u(t_i)}^{u(t_f)}du g(u)

Para resolverla tenes que hacer la integral.

espero que esto te sirva. si no, no dudes en repreguntar que trato de aclarar lo que sea necesario

saludos

g
En respuesta a Guzman Hernandez

Re: Primer parcial 2017 ej 1c y 1d

de Silvina Daniela Datz Helbling -

Sería así la cuenta?

La duda que me queda es, si la ecuación de movimiento hallada es en un entorno del instante inicial, puedo a partir de ella hallar una velocidad final limite?


Adjunto 20200520_110520.jpg
En respuesta a Silvina Daniela Datz Helbling

Re: Primer parcial 2017 ej 1c y 1d

de Ricardo Marotti -


En tu solución estás cometiendo un error, y es que llegás a una ecuación diferencial no lineal (tiene un término en u^2 ) y la estás resolviendo como si fuese lineal (solución de la homogénea más solución particular). Eso no es correcto. Para aplicar ese método de solución el cambio de variable correcto es  u( \varphi)= \dot{ \varphi }^2 , que si te lleva a una ecuación diferencial lineal. El cambio de variable que te sugería Guzmán es para transformar la ecuación en una de variables separables.Que es lo que hace en la solución del examen que está en la página de EVA. 

Para hallar la solución límite en la que  \dot{ \varphi } es constante, alcanza con hacer  \ddot{ \varphi } = 0 en la ecuación diferencial. 

Y el valor límite de la velocidad al que se llega es el mismo valor de la velocidad constante al que se había llegado en la parte b. Y la ecuación de movimiento obtenida valía mientras la velocidad fuese mayor que este valor (para que no cambie el signo de la normal). Por lo tanto en el intervalo de tiempo que la velocidad va decreciendo (la partícula se va frenando) sigue valiendo la ecuación de movimiento, porque la velocidad es mayor que el valor límite (que es el valor constante de la parte b) y la normal no cambia de signo. O sea la ecuación diferencial es válida en un entorno de tiempo que es mientras no cambie el signo de la normal, lo que no sucede en todo el movimiento posterior. 

Este ejercicio es parecido al Ejercicio No 10 del Práctico II, que fue resuelto en la clase de Zoom del lunes 30/3/2020. Podés ver más detalles en esa clase.