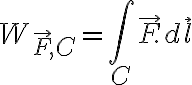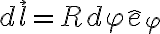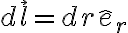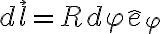Buenas, no logro calcular la intregral del trabajo, se que hay que hacerla en tramos pero no llego nada. Saludos
La definici'on de trabajo de una fuerza 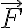 a lo largo de una curva
a lo largo de una curva 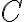 est'a dada por la integral de linea
est'a dada por la integral de linea
En este ejercicio queremos tomar 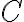 la curva cerrada de la figura. Si el trabajo de la fuerza que estamos considerando no es cero en esta curva, podemos concluir que la fuerza no es conservativa.
la curva cerrada de la figura. Si el trabajo de la fuerza que estamos considerando no es cero en esta curva, podemos concluir que la fuerza no es conservativa.
Para calcular el trabajo a lo largo de la curva conviene separar la curva en cuatro tramos, dos tramos radiales y dos arcos de circunferencia. el trabajo total va a ser la suma de los trabajos en cada uno de los tramos.
Veamos como calcular la integral en cada uno de los tramos. La clave es ver como parametrizar la curva y escribir el diferencial 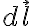 en cada tramo. Obviamente es conveniente utilizar coordenadas polares.
en cada tramo. Obviamente es conveniente utilizar coordenadas polares.
En los tramos curvos el diferencial 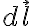 se puede escribir en t'erminos del radio del tramo
se puede escribir en t'erminos del radio del tramo  y el diferencial de arco
y el diferencial de arco 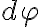 de la siguiente manera
de la siguiente manera
La integral queda en terminos de una integral en la variable  , siendo los limites de integracion
, siendo los limites de integracion 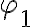 y
y  . Resta hacer el producto interno entre
. Resta hacer el producto interno entre 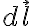 y la fuerza. Cuanto da este producto?
y la fuerza. Cuanto da este producto?
OJO: en realidad hay que tener cuidado con el sentido con el que se recorre la curva (esto cambia el signo del trabajo). Pero la respuesta a la pregunta de la linea anterior te va a indicar que esto no importa demasiado para los tramos curvos. si es importante para los tramos rectos, que describo a continuacion.
Vamos a ver como calcular el trabajo en uno de los tramos curvos, suponiendo que lo recorremos en el sentido de menor a mayor radio. En este caso el diferencial 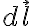 queda
queda
La variable de integracion es en este caso  y los limites son
y los limites son 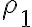 y
y 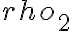 . Nuevamente para hallar el integrando debes hacer el producto escalar entre
. Nuevamente para hallar el integrando debes hacer el producto escalar entre 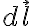 y la fuerza. Para hallar en el otro tramo recto usas la misma idea, teniendo cuidado con que si recorres la recta de afuera hacia adentro o de adentro hacia afuera cambia el signo, y tienes que ser consistente en como son los recorridos para formar una curva cerrada.
y la fuerza. Para hallar en el otro tramo recto usas la misma idea, teniendo cuidado con que si recorres la recta de afuera hacia adentro o de adentro hacia afuera cambia el signo, y tienes que ser consistente en como son los recorridos para formar una curva cerrada.
Te preguntaras tambien como se llega a estas formulas. Una forma de calcular una integral de linea a traves de una curva 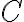 cualquiera es pensar que la integral se recorre con una trayectoria en funcion del tiempo dada por una funcion
cualquiera es pensar que la integral se recorre con una trayectoria en funcion del tiempo dada por una funcion 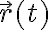 . Entonces la integral de linea puede escribirse
. Entonces la integral de linea puede escribirse
\int_C \vec{F}.d\vec{l} \) = \int_C \vec{F}.\vec{v}(d)dt \)
siendo 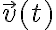 la velocidad asociada a
la velocidad asociada a 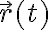 . Resulta que el resultado de la integral de linea (asumiendo que la fuerza solo depende d la posicion) no depende de la funcion
. Resulta que el resultado de la integral de linea (asumiendo que la fuerza solo depende d la posicion) no depende de la funcion 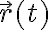 que uno elija. Una forma de llegar a las formulas que escribi antes entonces es tomando velocidad constante para los tramos rectos y velocidad angular constante para los tramos curvos.
que uno elija. Una forma de llegar a las formulas que escribi antes entonces es tomando velocidad constante para los tramos rectos y velocidad angular constante para los tramos curvos.
espero que esto te sirva. si necesitas aclarar algo no dudes en repreguntar.
saludos
g
Hola, traté de calcular el trabajo como explicaste ahi, es así como se hace?
va foto
gracias


En los tramos curvos tenés que observar que la curva que se recorre es perpendicular a la fuerza, por lo tanto el producto escalar involucrado en el trabajo es cero.
En los tramos rectos creo que te quedaron ambos con signo cambiado. La primitiva de 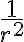 es
es 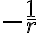 . Y primero sea evalúa en el límite superior y luego en el inferior, cambiado de signo.
. Y primero sea evalúa en el límite superior y luego en el inferior, cambiado de signo.
En los tramos curvos: entiendo ahora que lo decís que da 0 pero hay alguna manera de ver que es cero analiticamente? es decir, yo debería haber puesto el versor er cuando sustituí la expresión de la fuerza?
En los tramos rectos: sí tenes razón están mal evaluados ya lo corrijo
Perdón tantas preguntas siento que hay algunos conceptos que me quedan medios colgados, estoy cursando calculo vectorial y todo esto es bastante nuevo
Gracias
Como dijo Guzmán arriba, al calcular el trabajo, hay que integrar el producto escalar de la fuerza con el diferencial desplazamiento. En los tramos curvos se tiene que
Mientras que la fuerza es radial:
En los tramos curvos el producto escalar entre la fuerza y el diferencial desplazamiento es cero pues 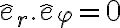 . Esa es la forma analítica de ver que el trabajo es nulo en esos tramos.
. Esa es la forma analítica de ver que el trabajo es nulo en esos tramos.