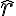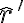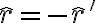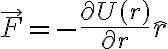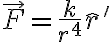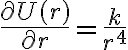Hola.
Para empezar, elegir el versor apuntando hacia el origen es en terminos practicos una muy mala idea.
Aun asi, el ejercicio se puede resolver de esa manera, pero tenes un error: el potencial como funcion de la distancia al origen queda el mismo elijas como elijas la direccion del versor. El motivo es el siguiente.
Para fijar ideas llamemos 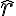 al versor que apunta desde O hacia la particula. Vos tomaste otro vesor, llamemosle
al versor que apunta desde O hacia la particula. Vos tomaste otro vesor, llamemosle 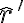 , que apunta desde la part'icula a el punto O. Obviamente
, que apunta desde la part'icula a el punto O. Obviamente 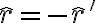 . Ahora bien, la formula para potencial asociado a una fuerza radial es.
. Ahora bien, la formula para potencial asociado a una fuerza radial es.
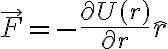
Nota que en la expresion anterior aparece 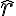 y no
y no 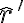 . Esto es por que el versor que tiene que aparecer es el que apunta en la direccion de
. Esto es por que el versor que tiene que aparecer es el que apunta en la direccion de  creciente, que es
creciente, que es 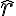 y no
y no 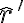 . esto es por la definicion de gradiente basicamente.
. esto es por la definicion de gradiente basicamente.
El punto es que cuando escribiste la fuerza a vos te quedo positiva en la direccion de 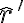 , es decir vos escribiste algo asi
, es decir vos escribiste algo asi
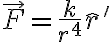
Ahora, para comparar con la primera ecuacion es conveniente usar que 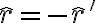 entonces
entonces

de lo que se deduce que 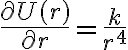 y se llega a la misma expresion para el potencial que si hubieras usado el otro versor.
y se llega a la misma expresion para el potencial que si hubieras usado el otro versor.
Una aclaracion conceptual/intuitiva: el potencial asociado a la fuerza, como funcion de la distancia al origen, no "sabe" de versores y direcciones de versores. La elecci'on de una base de versores u otra es algo arbitrario, que no influye en la fisica del problema.
matematicamente lo que estoy diciendo es que el gradiente se puede definir sin hacer referencia especifica a una base, si bien su expresion final si depende de la base