Buenas! No me doy cuenta como arrancarlo...
Hola,
Te tiro algunas ideas de como pensar este tipo de ejercicios. A medida que lo vayas haciendo te surgiran dudas mas especificas. En ese caso pregunta nuevamente y lo vamos discutiendo.
El punto clave es que la fuerza que actúa sobre el proyectil es lo que llamamos una fuerza central. Es decir, la fuerza sobre el proyectil tiene siempre dirección en la recta que va desde el proyectil al blanco. Esto tiene una consecuencia muy importante: el momento angular del proyectil con respecto al blanco en este problema se conserva. (vale la pena que repases el teorico para entender precisamente por qu'e esto es así )
El problema es claramente bidimensional. (Esto de hecho es una caracteristica de el movimiento bajo fuerzas centrales, debido a la conservacion del momento angular). Voy a usar coordenadas polares 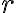 y
y 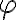 con origen en el blanco para describir el movimiento del proyectil. Voy a llamarle
con origen en el blanco para describir el movimiento del proyectil. Voy a llamarle  al origen de coordendas (punto donde se encuentra el blanco).
al origen de coordendas (punto donde se encuentra el blanco).
Calculemos el momento angular de la particula en terminos de las coordenadas polares:
El vector posición de la part'icula, medido en el sistema de coordenadas descrito anteriormente, es 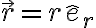 .
.
La velocidad de la particula está dada entonces por 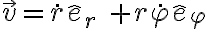 .
.
El momento angular de la particula con respecto al punto en que se encuentra el blanco esta dado entonces por
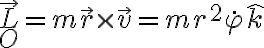 . Dado que
. Dado que 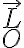 se conserva, podemos concluir que
se conserva, podemos concluir que 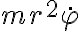 es constante en el tiempo. En particular, es igual a su valor en el instante inicial
es constante en el tiempo. En particular, es igual a su valor en el instante inicial 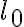 . Es decir que tenemos
. Es decir que tenemos
Donde 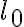 se puede hallar en terminos de las condiciones iniciales de la particula (velocidad con la que incide en el blanco desde el infinito y parametro de impacto inicial). La ecuacion anterior es sumamente importante, por que nos permite transformar el problema de un problema de dos grados de libertad a uno de un grado de libertad. Te resumo brevemente como es que esto sucede, para que lo intentes hacer por tu cuenta.
se puede hallar en terminos de las condiciones iniciales de la particula (velocidad con la que incide en el blanco desde el infinito y parametro de impacto inicial). La ecuacion anterior es sumamente importante, por que nos permite transformar el problema de un problema de dos grados de libertad a uno de un grado de libertad. Te resumo brevemente como es que esto sucede, para que lo intentes hacer por tu cuenta.
Si planteas la ecuacion de newton vas a tener dos componentes. La componente segun 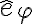 podes verificar que es precisamente equivalente a la ecuacion
podes verificar que es precisamente equivalente a la ecuacion 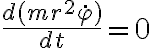 , que es justamente la conservacion de momento angular que discutimos antes.
, que es justamente la conservacion de momento angular que discutimos antes.
La componente radial de la ecuacion de newton involucra  ,
, 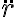 y
y 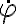 . El paso clave es que utilizando la conservacion de momento angular
. El paso clave es que utilizando la conservacion de momento angular 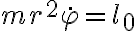 uno uede despejar
uno uede despejar 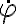 en funcion de
en funcion de  y enchufar esto en la ecuacion correspondiente a la componente radial de la ec de newton. Con esto, la ec de newton involucra solo
y enchufar esto en la ecuacion correspondiente a la componente radial de la ec de newton. Con esto, la ec de newton involucra solo  y sus derivadas!!! Es decir que logramos pasar de un problema de dos grados de libertad a una ecuacion diferencial que solo involucra
y sus derivadas!!! Es decir que logramos pasar de un problema de dos grados de libertad a una ecuacion diferencial que solo involucra  .
.
Te recomiendo que sigas en detalle por tu cuenta todos los pasos que esboce hasta ac'a. Luego de eso, todavia falta para resolver el ejercicio. Te resumo brevemente la estrategia a utilizar.
La ecuacion diferencial que uno obtiene para  de la forma mencionada anteriormente es dificil de resolver. Sin embargo, a nosotros no nos interesa
de la forma mencionada anteriormente es dificil de resolver. Sin embargo, a nosotros no nos interesa  en funcion del tiempo. Lo que interesa para responder la parte a) es la trayectoria de la particula, para lo cual basta con conocer en
en funcion del tiempo. Lo que interesa para responder la parte a) es la trayectoria de la particula, para lo cual basta con conocer en  en funcion de
en funcion de  . Para hallar esto conviene masajear un poco la ecuacion diferencial para r y transformarla de una ec dif para
. Para hallar esto conviene masajear un poco la ecuacion diferencial para r y transformarla de una ec dif para  con variable independiente
con variable independiente  a una ecuacion diferencial para la funcion
a una ecuacion diferencial para la funcion 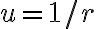 con variable independiente
con variable independiente  . (Es decir, la funcion
. (Es decir, la funcion  la pensamos como funcion de
la pensamos como funcion de  . ) Esta masajeada de la ec es lo que se conoce como el cambio de variable de Binet, que esta explicado en las notas. Resulta que la ec dif resulltatnte para
. ) Esta masajeada de la ec es lo que se conoce como el cambio de variable de Binet, que esta explicado en las notas. Resulta que la ec dif resulltatnte para  es facilmente soluble, lo que te permite hallar la trayectoria y eventualmente responder la pregunta.
es facilmente soluble, lo que te permite hallar la trayectoria y eventualmente responder la pregunta.
No te quise dar las cosas en demasiado detalle para que lo trates de hacer por tu cuenta. Espero que esto te sirva como empujon para arrancar. Cualquier cosa no dudes en volver a preguntar.
Saludos
g
Una consulta, en este ejercicio no hay fuerza peso? Porque si hubiera la posición no sería colineal con la fuerza neta siempre y no se conservaría el momento angular, no?
En efecto, no hay peso. La única fuera es la fuerza radial repulsiva que se menciona, porque, como escribís correctamente, si la fuerza neta no es radial no se trata de un movimiento central, y no se conserva el momento angular.
Hola, llegué a la ec diferencial u(θ), y la resolví con mis condiciones iniciales, pero tengo dudas sobre lo que tengo que hacer luego.
Vi en otras preguntas que igualan la ecuación a cero, por qué sería eso? Vi tambien que en la solucion se trabaja con la tangente, pero a mi se me anula el término de seno con las condiciones iniciales.
Dejo foto a partir de la ec diferencial. Gracias

Hola,
por lo que veo, tu ecuación diferencial está bien y la solución general de la homogénea así como la solución particular también.
El problema está en que:
i) las condiciones iniciales aplican a la solución total (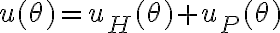 ) y vos las usaste sólo en la homogénea
) y vos las usaste sólo en la homogénea
ii) las condiciones iniciales no están bien; inicialmente, es decir, para 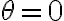 :
:
-la partícula está en el infinito 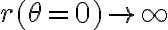 , que pasado a
, que pasado a 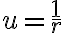 corresponde a decir
corresponde a decir 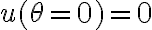
-la componente radial de su velocidad es (aprox.) 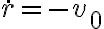 ; luego, como
; luego, como 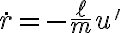 (ver Apuntes 2010 4.3) resulta que
(ver Apuntes 2010 4.3) resulta que 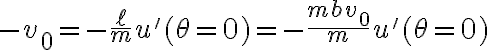 por lo que
por lo que 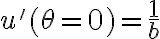 .
.
Fijate de corregir tus condiciones iniciales y usarlas en la solución total, con eso vas a hallar 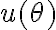 y de allí el resto del ejercicio.
y de allí el resto del ejercicio.
Suerte!
Ariel.
Perfecto, muchas gracias
