Buenas, no entiendo como resolver la parte b del ejercicio, para que la partícula llegue a "O" r=0 no? no me doy cuenta como usar esa condición junto con la energía o si sale por otro lado.
Gracias!
Buenas, no entiendo como resolver la parte b del ejercicio, para que la partícula llegue a "O" r=0 no? no me doy cuenta como usar esa condición junto con la energía o si sale por otro lado.
Gracias!
Hola, yo para hacer este ejercicio intérprete que para que la partícula alcanze el origen, r debe poder ser tan cercano a 0 como quieras.
Como la fuerza es central e isotropica la energía además del momento angular se conserva. Una vez que grafiques el potencial efectivo correspondiente vas a ver que tiene un máximo. Ahora si el valor de Energía (E) es menor que ese máximo, vas a tener que la gráfica del potencial efectivo y la recta de E=cte se cortan en 2 puntos, esos puntos son los puntos de retroceso.
Pará qué la masa que viene desde el infinito se acerque tanto a 0 como quieras no deben existir puntos de retroceso.
Yo lo pensé así, saludos
Hola,
El comentario de Federico est'a correcto. Como la fuerza es central, el momento angular se conserva. Adem'as, esta fuerza central es isotr'opica. Es decir, es de la forma 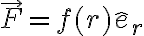 con
con 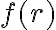 s'olo dependiente de
s'olo dependiente de 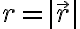 . Cuando una fuerza central es isotr'opica, es necesariamente conservativa. Por lo tanto en este problema tambi'en se conserva la energ'ia. Tener estas dos cantidades conservadas implica que el problema se puede reducir a un problema de un 'unico grado de libertad, la coordenada
. Cuando una fuerza central es isotr'opica, es necesariamente conservativa. Por lo tanto en este problema tambi'en se conserva la energ'ia. Tener estas dos cantidades conservadas implica que el problema se puede reducir a un problema de un 'unico grado de libertad, la coordenada  . Es m'as, la din'amica de la coordenada
. Es m'as, la din'amica de la coordenada  queda regida por una ecuaci'on de conservaci'on de la forma
queda regida por una ecuaci'on de conservaci'on de la forma
donde 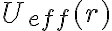 es el potencial efectivo, dado por
es el potencial efectivo, dado por
siendo 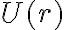 el potencial asociado a la fuerza central (que como dijimos es conservativa) y
el potencial asociado a la fuerza central (que como dijimos es conservativa) y 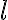 se puede hallar en funci'on de las condiciones iniciales.
se puede hallar en funci'on de las condiciones iniciales.
A los efectos de la parte b) de este problema, lo importante es que la ec de conservaci'on (1) se puede pensar como una ec de conservaci'on de la energ'ia para una part'icula que se mueve en una dimensi'on descrita por la coordenada  bajo la acci'on de un potencial
bajo la acci'on de un potencial 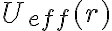 .
.
La clave para resolver la parte b) es la siguiente. Las condiciones iniciales del movimiento fijn 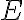 y
y 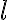 . Fijadas estas constantes, la ecuaci'on (1) te dice cuales van a ser las regiones en
. Fijadas estas constantes, la ecuaci'on (1) te dice cuales van a ser las regiones en  accesibles para la part'icula. Estas son aquellas donde
accesibles para la part'icula. Estas son aquellas donde 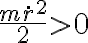 , o lo que es lo mismo, las regiones en
, o lo que es lo mismo, las regiones en  donde
donde 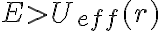 .
.
Si te fijas la forma del potencial efectivo para este problema, este tiende a menos infinito para  tendiendo a cero, tiene un m'aximo, y tiende a cero para
tendiendo a cero, tiene un m'aximo, y tiende a cero para  tendiendo a infinito. Llamemos a el m'aximo del potencial efectivo
tendiendo a infinito. Llamemos a el m'aximo del potencial efectivo 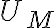 . Si
. Si 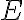 , entonces la condici'on
, entonces la condici'on 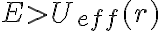 se va a cumplir en dos regiones en
se va a cumplir en dos regiones en  :
: 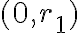 y
y 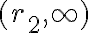 , siendo
, siendo 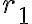 y
y 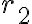 los puntos en que
los puntos en que 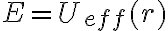 . Dado que la part'icula comienza su trayectoria en el infinito, su movimiento se va a ver limitado a la regi'on
. Dado que la part'icula comienza su trayectoria en el infinito, su movimiento se va a ver limitado a la regi'on 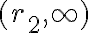 . Es decir, la particula va a partir desde el infinito, su radio va a ir disminuyendo a medida que se acerca al origen de fuerzas hasta que el radio llega al punto de retroceso
. Es decir, la particula va a partir desde el infinito, su radio va a ir disminuyendo a medida que se acerca al origen de fuerzas hasta que el radio llega al punto de retroceso 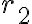 y ah'i se va a empezar alejar del origen de la fuerza central. Es decir, la part'icula no va a llegar al origen de la fuerza central.
y ah'i se va a empezar alejar del origen de la fuerza central. Es decir, la part'icula no va a llegar al origen de la fuerza central.
Para que esto suceda, es necesario que 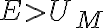 . En ese caso la region permitida es
. En ese caso la region permitida es 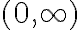 y la part'icula se acerca indefinidamente al origen de fuerzas.
y la part'icula se acerca indefinidamente al origen de fuerzas.
saludos
g