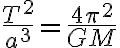Buenas, en esta parte para calcular la energía de la orbita de transferencia se me ocurrió que, como hay conservación de la energía, puedo calcularla en el momento que es tangente a la Tierra, usando la vel angular de la tierra y su radio, está bien pensarlo así? porque en la solución calcula la energía en el momento que la óriba de tranferencia es tangente a la órbita geoestacionaria
Gracias
Silvina, que tal?
Lo que decís es verdad, sin embargo, en este ejercicio, el objetivo del viaje es llegar a la órbita geo-estacionaria. Por lo tanto es importante usar el hecho de que la órbita de transferencia tiene que coincidir en un punto con la órbita geo-estacionaria. Es calculando la energía cuando coinciden estas órbitas que más adelante vas a poder encontrar la velocidad necesaria para que la cápsula se ubique en la órbita de transferencia que eventualmente la va a llevar a la órbita geo-estacionaria. Me explico?
Espero que te sirva!
Tomás
Gracias. Con respecto a la parte e de este ejercicio, no me doy cuenta como se hace
Para hacer la parte e de este Ejercicio hay que despreciar la parte radial de la velocidad, de forma que la órbita de transferencia es tangente a la circunferencia de la tierra y a la órbita geoestacionaria, como muestra la figura. Entonces el doble del semieje mayor de la órbita de transferencia va a ser igual a la suma del radio de la tierra y el de la órbita geostacionaria.
Luego para calcular el tiempo como el semiperíodo de la órbita de transferencia hay que usar la tercera ley de Kepler:
donde T es el período, a el semieje mayor de la órbita, G la constante de gravitación universal y M la masa de la tierra en este caso. Para calcular GM hay que observar que evaluando la fuerza gravitatoria en el radio de la tierra esto tiene que ser igual al peso.