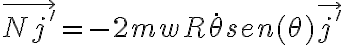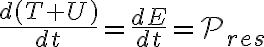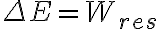Foro Práctico III

Hola!

En el ejercicio 2 de este parcial , en la parte c , intentamos lo siguiente:

1)Hallar la Velocidad absoluta de la particula con el teorema de roverball

2)La energía U_elastica =(kR^2)(1+cos(tita))

3)No actúa el peso

4)luego K=(m/2)(V^2) donde esta V esta compuesta de dos términos , uno en J' y otro en etita , con base en el paso 1

5)La única fuerza que hace trabajo es Nj' que es la componente de la normal que se sale del plano de la guía, y aplicando el teorema de coriolis 

encontramos que  $\vec{Nj'}=-2mwR \dot{ \theta } sen( \theta ) \vec{j'}$

6)igualar d(K+U)/dt al trabajo de la normal segun J' ,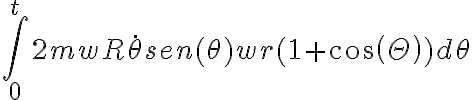$\int_{0}^{t}{2mwR \dot{ \theta } sen( \theta )}{wr(1+cos( \Theta ))} d\theta$ 

donde 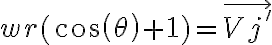$wr(cos( \theta )+1)= \vec{Vj'}$ es la velocidad de la particula según j'

¿Es este procedimiento correcto para hallar la ecuación de movimiento?