Hola,
No logro encontrar cual seria la correcta velocidad de la bala vista desde la tierra. En primera instancia supuse que solo tenia que sumar la velocidad de A ( velocidad del cohete) a la velocidad relativa de la bala.
Gracias
Es tal como decís, el cohete sólo se traslada con velocidad 
por lo que la velocidad de la partícula vista desde la Tierra será la suma de la velocidad de la bala relativa al cohete y la velocidad de transporte, que coincide con .
Saludos,
Ariel.
Hola, tengo la duda de por qué no se toma en cuenta el ω de la Tierra.
Hola Vanessa,
es una excelente observación!
El tema es que salvo que se indique en sentido contrario en algún tema en particular (fijate por ejemplo en la sección 2.3.1 de los Apuntes 2010), consideramos a la Tierra a todos los efectos como un sistema inercial, para lo cual despreciamos su rotación alrededor de su eje: con la rotación presente no podríamos tratarlo como inercial desde que cualquier punto sobre su superficie, salvo en los polos, sufre una aceleración inducida por esta rotación (despreciamos también su traslación alrededor del Sol, pero este efecto es aún menor que el de rotación sobre su eje).
Saludos,
Ariel.
Gracias,
Me cuesta entender cuándo los sistemas son inerciales/ no inerciales en la práctica. Si tengo un sistema S, uno S' y una partícula P: La partícula P puede estar acelerando respecto a S', pero mientras S' no acelere respecto a S, es inercial? Y si S' acelera respecto a S ya no es inercial, por tanto no puedo aplicar newton, ¿estoy en lo correcto?
Si S es inercial, S' será inercial si no se acelera respecto a S. O sea que se traslada con velocidad constante.
Los sistemas inerciales son aquellos en los que vale la segunda ley de Newton para todas las partículas. Así que si S es inercial:
donde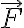 
es la fuerza neta y 
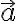es la aceleración absoluta (aceleración respecto a S) de una partícula cualquiera.
Si queremos que S' sea inercial tiene que valer la segunda ley de Newton en S':
donde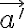 
es la aceleración relativa (aceleración respecto a S') de esa partícula arbitraria.
Luego para que S' sea inercial tendrá que valer que
para lo que para todas las partículas tendrá que valer que la aceleración de arrastre y la aceleración de Coriolis sean cero. Esto implica que la velocidad angular de S' respecto a S es cero. O sea que el sistema S' se traslada respecto a S con aceleración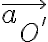 
. Pero esta aceleración también tiene que ser cero, para que la aceleración de arrastre lo sea. O sea que S' solo puede trasladarse respecto a S con aceleración nula, esto es, velocidad constante.
Muchas gracias!