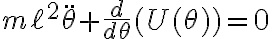Buenas tardes. En este ejercicio llego al resultado final, pero me surge una duda conceptual. Para que haya equilibrio debe ser  , verdad? Con las expresiones para velocidad y aceleración de este ejercicio, llego a la conclusión de que para que eso se cumpla, debe ser
, verdad? Con las expresiones para velocidad y aceleración de este ejercicio, llego a la conclusión de que para que eso se cumpla, debe ser 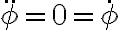 . Al imponer esto en la ecuación de movimiento, como en esta no aparece
. Al imponer esto en la ecuación de movimiento, como en esta no aparece  , siento que en ningún momento me estoy asegurando que
, siento que en ningún momento me estoy asegurando que 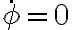 , si no que solo me aseguro que es constante. Por lo tanto, podría ser, dependiendo de las condiciones iniciales, que en realidad
, si no que solo me aseguro que es constante. Por lo tanto, podría ser, dependiendo de las condiciones iniciales, que en realidad 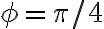 no fuera una posición de equilibrio ?
no fuera una posición de equilibrio ?
La idea es la siguiente: una posición es de equilibrio, si yo pongo la partícula en dicha posición con velocidad nula, ella se queda ahí. Eso implica que cuando las condiciones iniciales son esas (partícula en la posición de equilibrio, con velocidad nula) la aceleración tiene que ser nula (para que la velocidad sea constante y la partícula se quede ahí).
La posición puede ser de equilibrio, pero si al poner la partícula en esa posición, la velocidad inicial no es nula, la partícula no se va a quedar en ella. Para que permanezca en esa posición tiene que ser la velocidad inicial nula (si la posición inicial es la del equilibrio).
Por eso cuando buscamos posiciones de equilibrio hacemos velocidad y aceleración nulas, porque ambas deben serlo para que la partícula permanezca en ella. No quiere decir que si la velocidad es otra, la partícula permanezca allí, por más que la posición sea de equilibrio.
Entonces no te tenés que preocupar de que no estés haciendo la velocidad nula, porque es la condición inicial que precisamos para que la partícula permanezca en el equilibrio. Si la velocidad no es nula, no permanecerá allí por más que la posición inicial sea la del equilibrio. Siempre se precisa velocidad inicial nula (en la posición inicial de equilibrio) para que la partícula permanezca en ella.
Ahora lo que se demuestra en Apuntes R. Marotti Clase Pequeñas Oscilaciones, es que para que una posición sea de equilibrio, la energía potencial debe tener un extremo relativo; y viceversa, si una posición tiene un extremo relativo de la energía potencial es de equilibrio. Y si ese extremo relativo de la energía potencial es un mínimo, la posición de equilibrio es estable (que implica que si le erro por poco a la posición de equilibrio o a la velocidad en esa posición, el movimiento será oscilatorio en torno a ella). Si el extremo relativo es un máximo de la energía potencial, la posición de equilibrio es inestable (que implica que si le erro por poco a la posición de equilibrio o a la velocidad en esa posición, el movimiento será tal que la partícula se alejará de la posición de equilibrio).
Me quedó clarísimo! Muchas gracias!!
Olvidé aclarar que lo que decía en el último párrafo del mensaje mío anterior, acerca de los extremos de la energía potencial, vale para la energía potencial total de un sistema conservativo. Es decir, un sistema en que las fuerzas sean o de potencia nula, o conservativas (derivan de una energía potencial). No vale necesariamente en el caso que haya fuerzas residuales (no conservativas), como es el rozamiento o fuerzas que dependan del tiempo o la velocidad.
Claro, en el caso de que haya fuerzas residuales creo que pasa lo mismo pero con un potencial efectivo
Hola,
un detalle nomás con respecto al caso de fuerzas residuales: aún cuando no se conserve la energía vista desde un referencial inercial, vas a poder mantener el análisis para el equilibrio y estabilidad mediante un potencial efectivo en algunos casos como el de una guía lisa uniformemente acelerada (ejercicio III.8) o con velocidad angular constante (III.9).
Si tenés dependencia explícita en el tiempo (aceleración no uniforme, velocidad angular variable) ya no se puede hacer un análisis por energía potencial, lo mismo para cualquier caso en que la guía sea rugosa. Allí a lo que tenés que recurrir es a la 2da ley de Newton y eventualmente estudiar la ecuación de movimiento resultante con los elementos que detalla Ricardo en sus mensajes anteriores.
Saludos,
Ariel.
Buenas!
Eso último me hace preguntarme cómo se haría en ese caso para estudiar la estabilidad? Con segunda ley de Newton pero cómo en sí? Si no se puede hacer un análisis por energía potencial... o eso no es tema de este curso?
Hola,
comienzo por contestarte con el final de tu mensaje: en este curso vamos a estudiar la estabilidad de las posiciones de equilibrio en los casos en es viable a partir del potencial (o potencial efectivo según el caso): los mínimos del potencial son posiciones de equilibrio estable (la caracterízación de que sean un mínimo corre por cuenta de las herramientas de análisis funcional que tenés de cursos previos).
Ahora, como acercamiento extra (ver en los apuntes de Ricardo sobre pequeñas oscilaciones) podés hallar la ley horaria a partir de tu ecuación de movimiento (que pudiste sacar por 2da ley de Newton por ejemplo) y ver que, en la cercanía de una posición 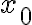 de equilibrio estable donde el potencial
de equilibrio estable donde el potencial 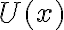 tenga una aproximación parabólica (
tenga una aproximación parabólica (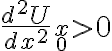 ), el sistema sigue una oscilación armónica (digamos que se comporta como un sistema masa-resorte). Ese movimiento es tan acotado como lo impongan las condiciones iniciales de cercanía al equilibrio, lo que es otra forma de caracterizar que se trata de una posición de equilibrio estable.
), el sistema sigue una oscilación armónica (digamos que se comporta como un sistema masa-resorte). Ese movimiento es tan acotado como lo impongan las condiciones iniciales de cercanía al equilibrio, lo que es otra forma de caracterizar que se trata de una posición de equilibrio estable.
Este acercamiento a estudiar la estabilidad a partir de la evolución temporal en la proximidad del equilibrio (es decir, ver si para una condición inicial arbitraria de proximidad el sistema se mantiene cerca de la posición de equilibrio o no lo hace) es claramente extensible a problemas donde no existe una energía potencial asociada, pero ese estudio es materia de otros cursos, por ejemplo Vibraciones y Ondas. Ya que preguntaste, está bueno igual tener en claro las alternativas.
Saludos,
Ariel.
Buenas, me queda la duda de qué exactamente es lo que me permite no tomar en cuenta θpunto al hacer la derivada segunda de la energía potencial. Y en general desde que parte puedo derivar en dU/dθ (esta es una duda que tengo en cada ejercicio, que tanto puedo simplificar al hacer la primer derivada. Si tomo desde la ec de movimiento, no estoy perdiendo informacion?) Disculpá si es la misma duda, pero no lo entendi.
Dejo fotos también de la parte A porque me queda una diferencia en el resultado por un factor de 4, y no encuentro el error.


Hola Vanessa,
tu pregunta tiene varias partes, voy contestando de acuerdo a como tenés desarrollado el problema y está en las imágenes:
i) el factor de 4 que te sobra proviene de que el vector posición de la masa 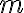 no está bien escrito y debería cumplir:
no está bien escrito y debería cumplir:
con lo que al derivar hallás la velocidad correcta y de ahí en más el ejercicio va a ir bien.
ii) La energía del sistema es:
y usando que esta cantidad se conserva en el tiempo (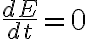 ) podemos derivar
) podemos derivar 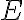 :
:
y obtener de allí la ecuación de movimiento (ojo de aquí en más porque ví en tu desarrollo que considerás la derivada de la energía cinética respecto de  y de
y de 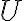 con respecto a
con respecto a  , vamos a ver cómo derivar correctamente).
Derivemos entonces la energía:
, vamos a ver cómo derivar correctamente).
Derivemos entonces la energía:
en cada término usamos la regla de la cadena adecuadamente:
donde el segundo término del producto del lado derecho es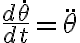 :
:
Para el siguiente término procedemos análogamente:
con lo que juntando los dos términos te queda:
o lo que es lo mismo:
siendo lo que multiplica a la ecuación de movimiento (
la ecuación de movimiento (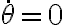 es una solución trivial que dice que la energía no varía si el sistema no se mueve nunca
y además viene desde el paso cero del planteo energético a partir de Newton):
es una solución trivial que dice que la energía no varía si el sistema no se mueve nunca
y además viene desde el paso cero del planteo energético a partir de Newton):
Hasta ahí las derivadas temporales que deberías revisar. Al llegar a la ecuación de movimiento fijate que las posiciones de equilibrio (correspondientes a todas las derivadas temporales nulas, es decir en este caso 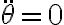 ) se dan para
) se dan para 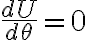 ,
y allí conectamos con tus preguntas acerca de la energía potencial:
,
y allí conectamos con tus preguntas acerca de la energía potencial:
iii) los puntos de equilibrio, en sistemas donde se conserva la energía (o no conservativos preintegrables) son aquellos donde la energía potencial (o potencial eficaz) tiene extremos relativos:
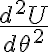 alrededor de la posición de equilibrio y si esta derivada segunda es no nula, inferir de qué tipo de extremo se trata; si fuera nula, se aplican otras
herramientas de análisis o se ven derivadas de mayor orden).
alrededor de la posición de equilibrio y si esta derivada segunda es no nula, inferir de qué tipo de extremo se trata; si fuera nula, se aplican otras
herramientas de análisis o se ven derivadas de mayor orden).No sé si pude capturar todas tus dudas, cualquier cosa volvé a preguntar nomás.
Saludos,
Ariel.

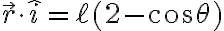
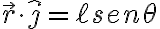
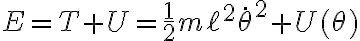
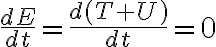
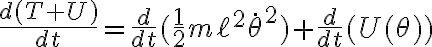
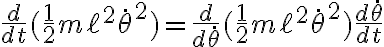
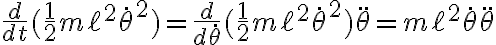
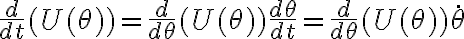
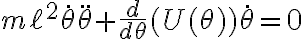
![[m\ell^2\ddot{\theta}+\frac{d}{d\theta}(U(\theta))]\dot{\theta}=0 [m\ell^2\ddot{\theta}+\frac{d}{d\theta}(U(\theta))]\dot{\theta}=0](https://eva.fing.edu.uy/filter/tex/pix.php/c5d77697fb50ae9918f0c4d510fdcdb8.gif)