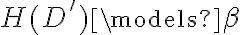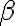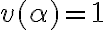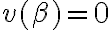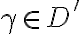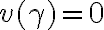Lógica: Demostracion de Correccion, introduccion del implica

Buenas,

Viendo la primera clase de correccion y completitud, en el momento que se demuestra la correccion y se hacer el paso inductivo de la introduccion del implica me queda la siguiente duda.
En el punto 2 (en la foto) se dice basicamente H(D') es o bien igual a H(D) o bien es H(D) + Alfa. Y despues la demostracion prueba la conclusion para los dos casos. Mi duda es: en el caso que Alfa no pertenece a H(D') , porque no podria haber una valuacion donde:
v(phi)=1 (para todo phi perteneciente a H(D)) pero v(alfa)=1 y v(beta)=0.
Basicamente no entiendo el paso logico del punto 2 al punto 3 (en la foto).
Gracias.

Adjunto Screen Shot 2020-05-03 at 10.26.07 AM.png

Re: Demostracion de Correccion, introduccion del implica

de Fernando Carpani - lunes, 11 de mayo de 2020, 13:15

Hola.

Esto ya lo respondimos en la clase de consulta, pero sólo para que quede aquí, trato de responderlo de nuevo.

La hipótesis en este caso es que $H(D') \models \beta$ . Esto no es otra cosa que la garantía de que cualquier valuación tal que hace verdaderas a todas las fórmulas de H(D'), tiene que hacer verdadera a $\beta$ .

Y esto es independiente totalmente de cómo estén formadas las hipótesis de D'.

Por lo tanto, ese caso que tiene a $v(\alpha)=1$ y $v(\beta)=0$ , tiene que tener también alguna hipótesis $\gamma \in D'$ tal que $v(\gamma) = 0$ . De lo contrario no se cumpliría la hipótesis que teníamos.

Espero que haya quedado más claro.

Saludos

FDO.