Buenas
No me queda claro porque en el ej 11 se conserva el momento angular. Si planteo la derivada de L, llego a que es el producto vectorial r x F, entonces estos deberían ser colineales para que sea 0, pero no entiendo porque esto es así.
Gracias
Es que en este ejercicio no se conserva el momento angular total. No es un ejercicio de movimiento central. Lo que se puede demostrar es que se conserva la componente del momento angular en O según el eje del cono. O sea, solo se conserva una componente del momento angular. Esto es básicamente lo que pide demostrar en la parte b a partir de la segunda ley de Newton.
También se puede observar que los momentos de ambas fuerzas (el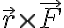 
que vos planteas), del resorte y de la reacción normal al cono, son perpendiculares al eje del cono. Por lo que si proyecto la derivada del momento angular según la dirección del eje del cono, eso si da cero. Y como la dirección del eje del cono es constante, esto implica que la proyección del momento angular según el eje del cono es constante.