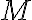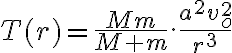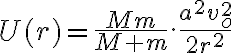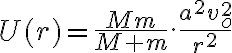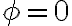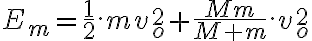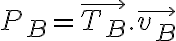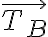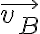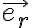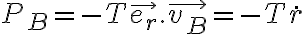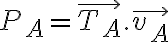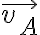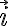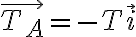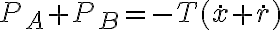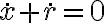Te estás equivocando en que la energía potencial no se suma: o sea no es el doble de la energía potencial sobre una partícula. Te lo voy a justificar demostrándote que la potencial total (actuando sobre ambas masas) de la tensión del hilo es nula.
Primero calculemos la potencia de la tensión del hilo que actúa sobre la partícula B:
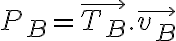
donde 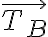 es la tensión del hilo actuando sobre B, y
es la tensión del hilo actuando sobre B, y 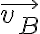 es la velocidad de esta partícula. Si le llamo
es la velocidad de esta partícula. Si le llamo 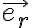 a un versor según la dirección radial de la partícula B:
a un versor según la dirección radial de la partícula B:  . Luego:
. Luego:
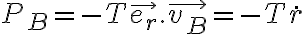
donde r es la coordenada radial de B.
Para la partícula A la potencia de la tensión del hilo es:
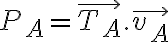
donde  es la tensión del hilo actuando sobre A, y
es la tensión del hilo actuando sobre A, y 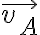 es la velocidad de esta partícula. Si le llamo
es la velocidad de esta partícula. Si le llamo 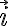 a un versor según la dirección radial de la partícula A:
a un versor según la dirección radial de la partícula A: 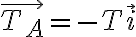 , donde T es la misma de arriba.
, donde T es la misma de arriba.

donde x es una coordenada radial para la partícula A.
Luego la potencia total de la tensión del hilo es:
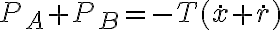
Pero por ser el hilo inextensible x + r = L constante (donde L es la longitud del hilo). Luego 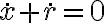 y la potencia total de la tensión del hilo es nula. Como no hay otras fuerzas la energía mecánica total será la energía cinética, que se conserva porque la única fuerza que actúa es de potencia total nula. Y entonces será igual a la energía cinética inicial.
y la potencia total de la tensión del hilo es nula. Como no hay otras fuerzas la energía mecánica total será la energía cinética, que se conserva porque la única fuerza que actúa es de potencia total nula. Y entonces será igual a la energía cinética inicial.