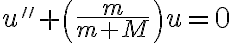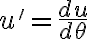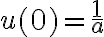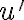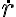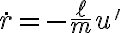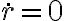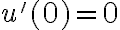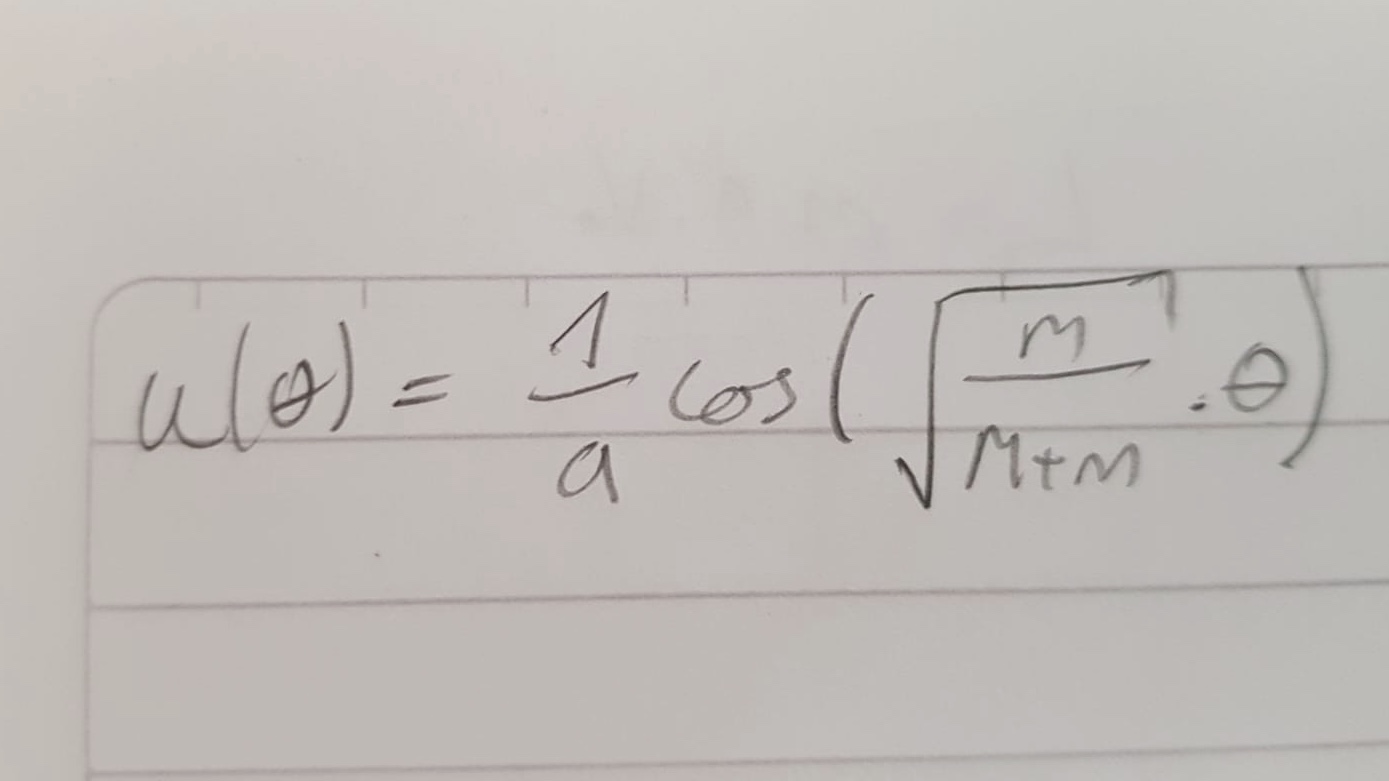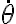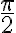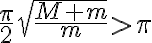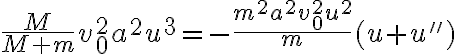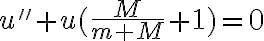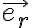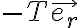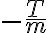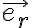Ejercicio 3b

Ejercicio 3b

de Federico Gomez Villanueva -
Número de respuestas: 9
Buenas,

Luego de obtener la ecuación de movimiento del ejercicio, apliqué las formulas de Binet y llegué a una ecuación lineal de segundo orden homogénea de la forma: 

(m+M)u”+mu=0 

Mi problema surge a la hora de escribir las condiciones iniciales de dicha ecuación; Sé que u, por Binet, se escribe como u(ψ)=1/r(ψ) ;siendo ψ en ángulo entre la horizontal y OB y r la distancia desde 0 a B. Pude obtener una de ellas la cual calculé como:

u(ψ=0) = 1/r(ψ=0) = 1/a 

La otra condición sería la correspondiente a velocidad, o sea u’(ψ=0), la cual no le puedo encontrar un valor. Por letra tengo el dato de que la velocidad inicialmente en B es perpendicular a OB pero no se si se debe aplicar aquí o no.

Tambien de paso quisiera saber si estoy por el camino correcto porque mi objetivo es encontrar la u(ψ) para luego ver como determinar la condición que se me pide.



En respuesta a Federico Gomez Villanueva

Re: Ejercicio 3b

de Ariel Fernández -

Hola Federico,

primero que nada, vas muy bien!

La ecuación diferencial que tenés que resolver:

u'' +\left(\frac{m}{m+M}\right)u=0

es de segundo grado, por lo que necesitás una condición inicial sobre u y otra sobre su derivada u'=\frac{du}{d\theta}

(ojo que no es una velocidad, es la derivada respecto a la coordenada angular \theta).

Sobre u ya tenés que u(0)=\frac{1}{a}; para u' te conviene ver para este problema y varios más la relación con

\dot{r}, que aparece en la deducción misma de las ecuaciones de Binet (ver por ej. Apuntes 2010, 4.3):

\dot{r}=-\frac{\ell}{m}u'

Como la velocidad inicial es perpendicular al vector posición no tiene componente en \hat{e}_r, por lo que, comparando con la velocidad en coordenadas polares:

\vec{v}=\dot{r}\hat{e}_r+r\dot{\theta}\hat{e}_{\theta}

resulta \dot{r}=0 y en consecuencia u'(0)=0.

Suerte con el resto del ejercicio!

Ariel.
En respuesta a Ariel Fernández

Re: Ejercicio 3b

de Juan Manuel Romero Yalinskas -

Resolviendo la ecuacion diferencial llego a lo siguiente:

.

No entiendo como seguir el ejercicio.

En respuesta a Juan Manuel Romero Yalinskas

Re: Ejercicio 3b

de Ricardo Marotti -


Esa solución es correcta, suponiendo que tu θ corresponde con el φ de la figura. 

Para seguir hay que observar que cuando el argumento del coseno se va a  \frac{ \pi }{2} , el coseno se hace 0. Eso es u = 0 y r tenderá a infinito. De la conservación del momento angular, cuando r tiende a infinito,  \dot{ \theta } tiende a cero. O sea que θ tiende a una constante. Esto implica que habrá una asíntota para el valor de θ que hace el argumento del coseno igual a  \frac{ \pi }{2} . Hay que asegurar que esa asíntota se de después de θ = π, porque si se da antes la partícula no llega a  θ = π. 
En respuesta a Ricardo Marotti

Re: Ejercicio 3b

de Pablo Ezequiel Gomez Ortiz -

Buenas tardes, llegue al mismo resultado pero no logré entender que es lo que tengo que hacer para hallar la condición.

En respuesta a Pablo Ezequiel Gomez Ortiz

Re: Ejercicio 3b

de Juan Tomas Urruzola Abdala -

Buenas! La lógica es la siguiente, vos sabés que cuando el argumento del coseno sea igual a pi/2, entonces u=0, lo que implica que r se va a infinito. Como el momento angular es constante, si r se va a infinito, phi(punto) tiene que irse a cero, por lo tanto: una vez que el argumento sea pi/2, el ángulo deja de variar y r se va a infinito.

Nosotros queremos que el ángulo llegue a valer pi. Por lo tanto, tiene que llegar antes de que el argumento sea pi/2. Es decir que cuando el argumento sea efectivamente pi/2, queremos que el ángulo sea mayor o igual a pi.

En definitiva, queremos que  \frac{ \pi}{2} \sqrt{ \frac{M+m}{m} } > \pi

Quedó más claro?
En respuesta a Juan Tomas Urruzola Abdala

Re: Ejercicio 3b

de Nahuel Borsil Pastorino -

Hola, no estaría llegando a la ecuación correcta.

Usé la definición de aceleración radial de Binet.

a_r= \frac{T}{m}= -\frac{l^2u^2}{m^2} (u+u'') uso m porque sería la masa de la partícula B que es la que interesa para esta parte.

entonces:  \frac{M}{M+m}v_0^2 a^2u^3=- \frac{m^2 a^2v_0^2u^2}{m} (u+u'')

Finalmente la ecuación me queda:  u''+u( \frac{M}{m+M}+1 )=0

En qué me equivoqué?
En respuesta a Nahuel Borsil Pastorino

Re: Ejercicio 3b

de Ricardo Marotti -


Tenés un error en el sentido de la tensión del hilo. El hilo siempre está tenso, o sea que la fuerza del hilo es hacia la polea. Así que si le llamo  \vec{e_r} a un versor según la dirección radial, la fuerza del hilo sobre la masa B es  - T \vec{e_r} . Así que el primer miembro de tu primer ecuación debe ser  - \frac{T}{m} . La componente de la aceleración radial de Binet es según   \vec{e_r} .