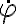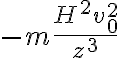Hola,
Quería hacer una pregunta sobre este ejercicio. En la parte a pide hallar las ecuación de movimiento de la masa puntual m, para esto demostré que se conservaba L y plantee newton despejando así la ecuación de movimiento en función de z.
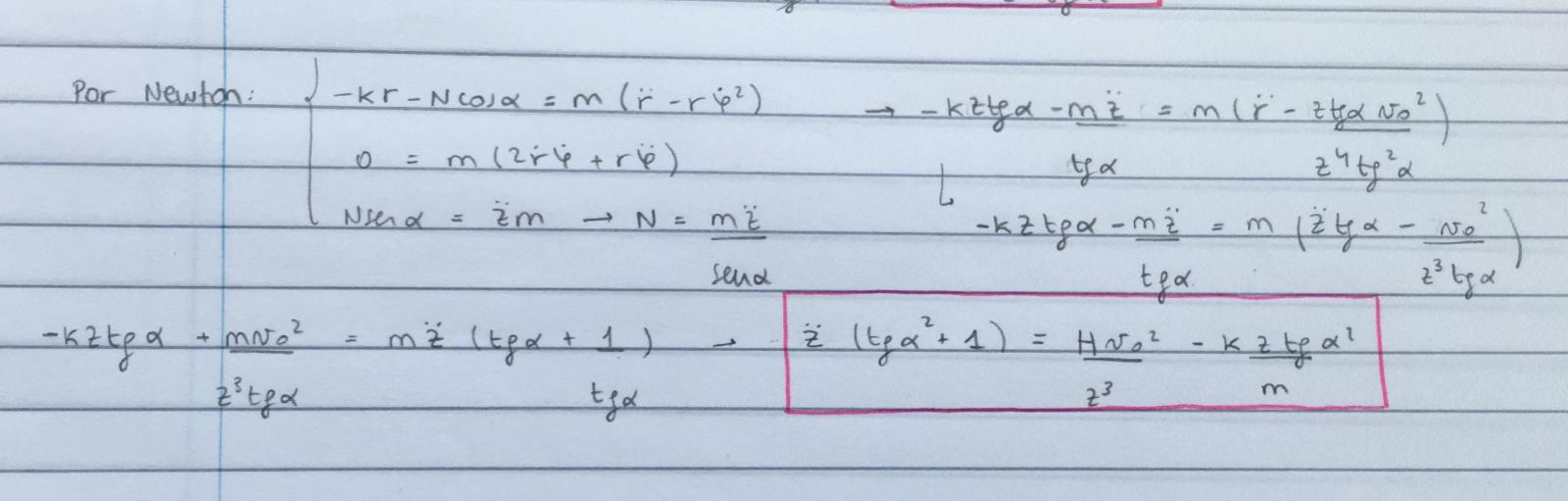
En la parte b me piden "Observe que no existe ninguna fuerza aplicada en la dirección perpendicular al eje del cono que es tangencial a su superficie, por lo que la aceleración de la partícula en dicha dirección sera nula. Preintegre la ecuación correspondiente y halle, a partir de dicha preintegral, la relación que vincula la velocidad angular fi punto de la partícula en torno al eje del cono con la coordenada z"
Y lo que hice para esta parte fue preintegrar la ecuación de movimiento y esto no se si es correcto, porque en las soluciones lo hacen por energía, aunque coincide mi resultado con ello. De todas formas, me gustaría saber si está correcto.
Por último en la la parte c pide despejar la ecuación diferencial para z(t) con las partes halladas en a y b, pero no entiendo como hacerlo con la información que ya tengo
Gracias
Saludos
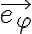
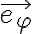
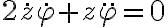
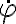
![m \ddot{z} [1+ (tg \alpha )^2 ] - mz (tg \alpha )^2 \dot{ \varphi }^2=-k(tg \alpha )^2 z](https://eva.fing.edu.uy/filter/tex/pix.php/2fa0c80732523cd285993523ded96713.png "m \ddot{z} [1+ (tg \alpha )^2 ] - mz (tg \alpha )^2 \dot{ \varphi }^2=-k(tg \alpha )^2 z")
