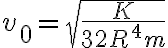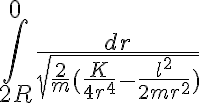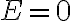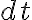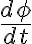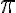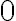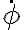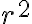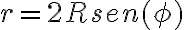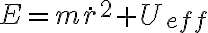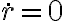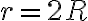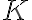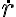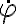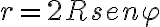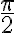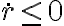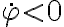Estimados Santiago y Nahuel: buena colaboración!
el paso clave sin dudas, tanto si quieren hallar el tiempo a partir de despejar i) 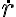 de la conservación de la energía o ii)
de la conservación de la energía o ii) 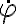 del momento angular, es usar la forma polar de la curva:
del momento angular, es usar la forma polar de la curva: 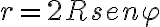 y pasar a integrar en el ángulo entre
y pasar a integrar en el ángulo entre 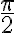 y
y  .
.
Importante acerca de los signos para que les de un tiempo positivo, como debe ser!:
i) 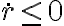 : la partícula se acerca al origen siempre (esto es para tener cuidado al despejar de la conservación de la energía la raiz con su signo correcto)
: la partícula se acerca al origen siempre (esto es para tener cuidado al despejar de la conservación de la energía la raiz con su signo correcto)
ii) 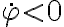 : el ángulo decrece en el tiempo
: el ángulo decrece en el tiempo
Saludos y suerte con las cuentas!
Ariel.
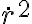 de la energía mecánica total, con lo que
de la energía mecánica total, con lo que 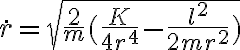 y de ahí integrar r entre 2R y 0 y dt por el otro lado. La integral de dr queda con una singularidad en 2R (cuando
y de ahí integrar r entre 2R y 0 y dt por el otro lado. La integral de dr queda con una singularidad en 2R (cuando 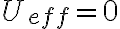 ) y pensé que seguramente la integral divergiría pero por el criterio de comparación por paso al límite resultó ser equivalente a
) y pensé que seguramente la integral divergiría pero por el criterio de comparación por paso al límite resultó ser equivalente a 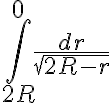 , que converge.
, que converge.