Este Ejercicio se puede hacer de dos formas diferentes:
la primer forma es observando que se conserva la energía y la componente según el eje del cono del momento angular.
la segunda es solo aplicando la segunda ley de Newton y obteniendo toda la información de allí.
Se puede hacer por cualquiera de los dos métodos, pero la letra está guiada para intentar hacerlo de esta segunda forma. Así las ecuaciones de movimiento que se refiere en la parte a son las que surgen de escribir la segunda ley de Newton. Pueden ser tres ecuaciones, en dos de ellas aparece la normal y se puede despejar la normal de una de ellas y sustituirla en la otra, como hacés en tu desarrollo. O más directamente se puede proyectar la ecuación de Newton según los versores 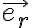 y
y 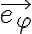 de coordenadas esféricas (que son las dos direcciones tangentes al cono liso). Así se obtienen dos ecuaciones de movimiento en z y φ.
de coordenadas esféricas (que son las dos direcciones tangentes al cono liso). Así se obtienen dos ecuaciones de movimiento en z y φ.
En la parte b refiere a tomar una de ellas, la que se obtiene de proyectar según 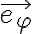 y preintegrarla. Esta es:
y preintegrarla. Esta es:
que es equivalente a la segunda ecuación que escribís en tu segunda figura. Al preintegrarla se obtiene la ecuación que corresponde a la conservación del momento angular: la ecuación de tu primer figura. O sea, como en movimiento central, la componente según 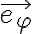 de la ecuación de Newton es equivalente a la conservación del momento angular (en este problema solo se conserva la componente según el eje del cono del momento angular).
de la ecuación de Newton es equivalente a la conservación del momento angular (en este problema solo se conserva la componente según el eje del cono del momento angular).
Hasta aquí no hay que usar el teorema de la energía.
En la parte c, se refiere a sustituir 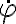 en la otra ecuación de movimiento. Que a mi me quedó:
en la otra ecuación de movimiento. Que a mi me quedó:
O sea que al sustituir 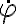 el segundo término será igual a
el segundo término será igual a
En este término tengo una diferencia con lo que te dio a vos. Ahí no veo en la foto si tu z está al cubo o al cuadrado. Si está al cubo el resultado está mal dimensionalmente. Debe ser un H^2 en el numerador. Creo que ese H al cuadrado ya te falta en la primer ecuación de la derecha de tu segunda foto.
Esta ecuación se puede obtener alternativamente de plantear el teormea de la energía, sustituir 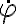 y luego derivar respecto al tiempo.
y luego derivar respecto al tiempo.

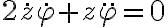
![m \ddot{z} [1+ (tg \alpha )^2 ] - mz (tg \alpha )^2 \dot{ \varphi }^2=-k(tg \alpha )^2 z m \ddot{z} [1+ (tg \alpha )^2 ] - mz (tg \alpha )^2 \dot{ \varphi }^2=-k(tg \alpha )^2 z](https://eva.fing.edu.uy/filter/tex/pix.php/2fa0c80732523cd285993523ded96713.gif)