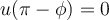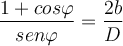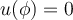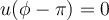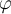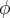Re: Ejercicio 4 parte a

Re: Ejercicio 4 parte a

de Leandro Jair Machado Da Silva -
Número de respuestas: 2

Buenas, decidí continuar con los otros ejercicios para no atrasarme. Ahora que vuelvo a intentar este, logro llegar al resultado de la parte b, tomando el resultado de la parte a (sigo sin llegar a la relación correcta). Por lo tanto, me gustaría saber si mi ecuación diferencial es correcta: 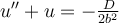 u''+u=-\frac{D}{2b^2} . Al resolverla llego a  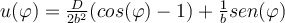u(\varphi)=\frac{D}{2b^2}(cos(\varphi)-1)+\frac{1}{b}sen(\varphi) . Al igualar a 0 y despejar, llego a que  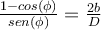\frac{1-cos(\phi)}{sen(\phi)}=\frac{2b}{D} , aquí uso que  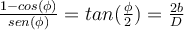\frac{1-cos(\phi)}{sen(\phi)}=tan(\frac{\phi}{2})=\frac{2b}{D} (relación matemática que busqué en internet por si estaba usando la inversa). Perdón las molestias, realmente no encuentro mi error :(
En respuesta a Leandro Jair Machado Da Silva

Re: Ejercicio 4 parte b

de Ariel Fernández -

Hola Leandro,

tu 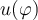u(\varphi) está perfecto acorde a que tu 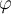\varphi inicial sea cero. En esa medida, el ángulo 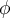\phi se corresponde con

u(\pi-\phi)=0

y te lleva a:

\dfrac{1+cos\varphi}{sen\varphi}=\dfrac{2b}{D}

(no sé si tenés un error en qué ángulo evaluás 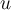u o en algo de la operativa trigonométrica)

Fijate por favor si con esto se te arregla el signo que tenés mal y te lleva a otra ec. para 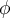\phi (si elegiste 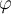\varphi inicial como 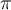\pi, cambia un poco 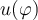u(\varphi) y la condición sobre el ángulo en que se va a infinito la partícula, pero la ecuación para 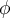\phi debe ser la misma).

Saludos,

Ariel.