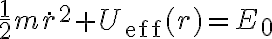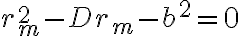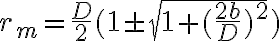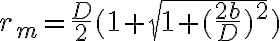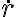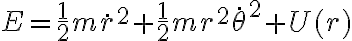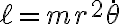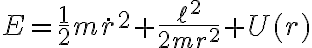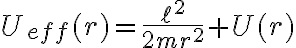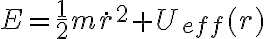Para hallar el r mínimo, busque el máximo de la función U(φ), este es en el angulo φ= tg-1(2b/D), cuando sustituyo este valor en r(φ) no llego a la solución. Debería hacerlo por otro lado ?
Los extremos del potencial te dan los puntos de equilibrio (donde la fuerza neta es cero), no es lo mismo que el punto de acercamiento máximo (donde en este caso de hecho no lo es).
En este caso en vez de los extremos del potencial querés estudiar los extremos de la función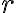 
, y para eso tenés que mirar la derivada. Podés usar conservación de la energía,
despejar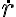 
en función de 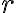y ver cuándo se hace cero. Esta es la distancia de acercamiento máximo y cuando la partícula empieza a retroceder.
Pero mi U(φ) no es el potencial, es U(φ)= 1/r(φ). Esta ecuación ya la tengo de la parte anterior y creo que que tendría que funcionar porque cuando U es máximo es porque r es mínimo. Estoy en lo correcto o me equivoco?
Buenas, yo tampoco logro llegar al resultado de la parte b, incluso en la parte a me queda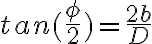 
(relación inversa a la de la respuesta) y no encuentro mi error. En la parte b, planteando por energía como sugeriste, me queda una ecuación de segundo grado para hallar R y por lo tanto no me queda lo de la solución, quizás sea lo mismo o no sé, me queda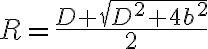 
En respuesta a Leandro Jair Machado Da Silva
Re: Ejercicio 4 parte b
Leandro, Sebastián, como andan? Les aconsejo seguir el camino que les plantea Esteban, ya que es el más directo para llegar a la expresión de la solución.
Lo que plantea Sebastián no está mal, simplemente se llega a una expresión más difícil de trabajar, pero conceptualmente está bien.
A vos Leandro te aconsejo revisar un poco las cuentas porque tenés efectivamente el inverso a lo que deberías tener, una vez que corrijas eso ya está! Si tomás la solución a la ecuación de segundo grado y le acomodás un poco los términos ya te queda, intenta sacar para afuera un D/2 como el de la solución y listo.
Suerte y cualquier cosa no duden en preguntar de nuevo!
Tomás
Intente hacerlo por la energia como dijo Esteban y llego a:
r2 - b2 = Dr
Probe despejar b de la parte a del ejercicio y sustituirlo en la ecuacion pero no llego a nada y no entiendo como seguir.
Juan, como va? Esa ecuación a la que llegaste está bárbara, ahora tenés que resolverla (es un polinomio de segundo grado) y si operás un poco vas a lograr llegar a la expresión de la solución. Te aconsejo, que, una vez que escribas la solución del polinomio, saques un factor D/2 para afuera y ahí uses el resultado de la parte a para hacer aparecer el ángulo.
Fijate si con eso llegás!
Llegue a la respuesta, pero con un ± antes del 1/sen(ρ/2). Porque la respuesta tiene un +, ya que restando obtendria el radio mas chico?
Bien! El resultado con el - te quedaría un r negativo, así que para que tenga sentido físico, tomamos el positivo.
Hola como te va ?, no entiendo porque quedaria negativo si tengo 1-(1/sen^2) en ese caso me daria el radio minimo.
No comprendo el argumento para seleccionar el positivo.
Desde ya gracias
Hola Facundo,
la ecuación que satisface la distancia mínima (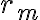
) al centro de fuerzas es tal como está en algún mensaje anterior:
,
cuyas raíces son:
que tal como dice Tomás en un mensaje anterior sólo admite una raiz positiva (que es lo que tiene sentido físico), ya que el radicando es mayor a 1:
.
Usando el resultado de la parte a):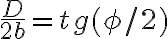 
y un poco de cuentas se llega a la solución, pero no hay nada ambiguo, la 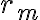que es raiz con sentido físico es una sola.
Saludos,
Ariel.
Buenas !
¿es esto lo que propones ?
https://drive.google.com/file/d/1ulUqOYkOE6V5pDIr4L406Clm55WN7wjr/view?usp=sharing
(te paso por drive porque la imagen es muy pesada para eva ,)
Gracias!
Buenas! La idea es esa si, sin embargo tenés un pequeño error en el término de la energía potencial de la fuerza repulsiva. Vos pusiste esa energía potencial con un r-2, pero en realidad es la fuerza la que tiene esa dependencia en r, la energía potencial debería quedarte con un r-1.
Fijate si por ahí sale!
Vi que efectivamente calculaste el potencial, pero se ve que te confundiste y en la expresión de la energía pusiste la fuerza en vez del potencial! Si corregís eso deberías llegar bien.
Suerte!
Buenas, no termino de entender por qué en el término de energía cinética solo aparece 
. No habría que considerar también la componente tangencial de la velocidad?
Hola Guillermo,
estamos considerando toda la energía cinética.
Tomemos como punto de partida la coservación de la energía total (ver por ej. ec. 4.8 de los Apuntes 2010):
.
Usando luego la conservación del momento angular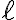 
(ec. 4.6):
podés sacarte de arriba 
en la conservación de la energía y quedarte con la siguiente expresión (ec. 4.9):
,
que involucra solamente a la coordenada 
y su derivada primera. A la suma de los últimos dos términos le llamamos potencial efectivo (o eficaz):
y la conservación de la energía queda así:
.
En esta última expresión, que es la que les sugiere de partida Esteban en unos mensajes anteriores, está involucrada toda la energía cinética ya que dentro del momento angular 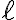con el que escribís 
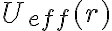está presente la componente tangencial de la velocidad. Es una forma además extremadamente útil para ver la evolución efectiva de
sin mezclarse con lo que pasa en la coordenada angular y hallar
por ejemplo el acercamiento máximo de la partícula al centro de fuerzas,
tal es el caso de esta parte de este ejercicio)
La confusión de pronto te surge por el hecho de que la conservación de la energía expresada así sólo involucra a la coordenada radial y su derivada, pero es toda la energía cinética la que que está involucrada en la conservación de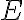 
en la ecuación de partida de este mensaje.
Saludos,
Ariel.