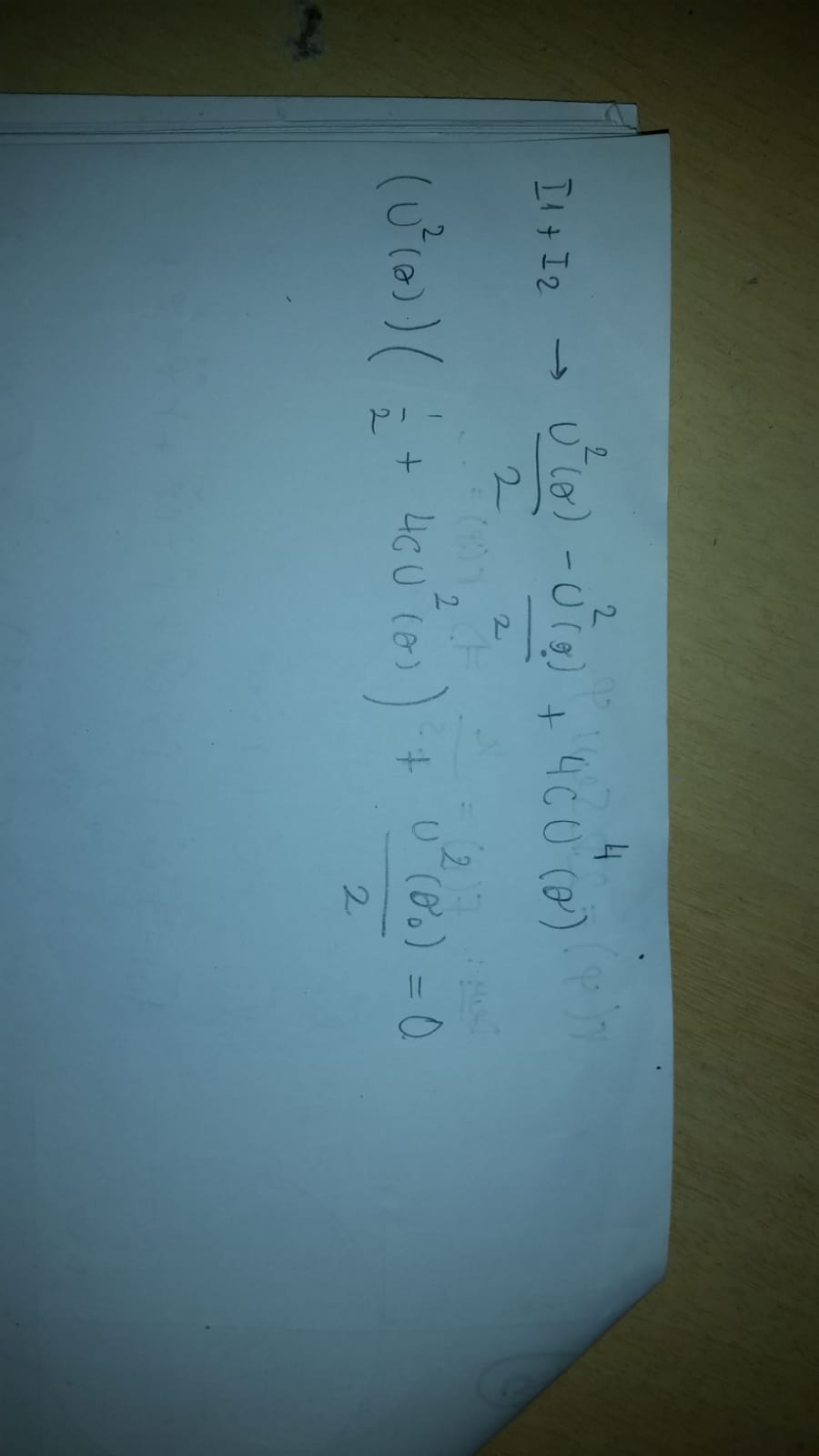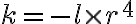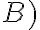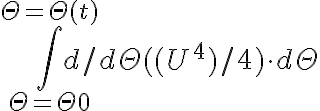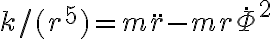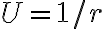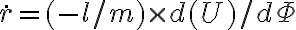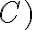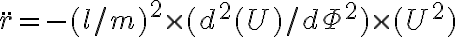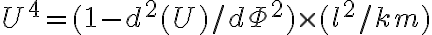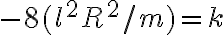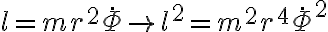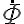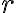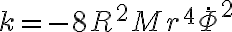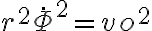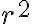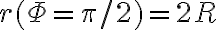Bien, respecto al método de substituir F y r por sus expresiones, por lo que vi tenés un error en la segunda derivada de r respecto al tiempo, esto se debe a que hiciste aparecer un r2 en la primera derivada de r respecto al tiempo y al derivar nuevamente la trataste como una constante.
Lo que te recomiendo para esto es pasarte a las ecuaciones de Binet, te van a simplificar la vida porque vas a tener derivadas respecto a θ y no respecto al tiempo.
Respecto al método de resolver la integral, lo pruebo y te digo! La verdad no había pensado en hacerlo así.
Fijate si con lo primero que te dije llegás bien!
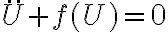 entonces multipliqué por \dot{U} , y mi duda sería si estoy bien encaminado.
entonces multipliqué por \dot{U} , y mi duda sería si estoy bien encaminado.