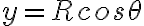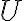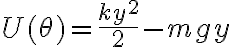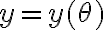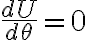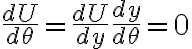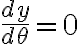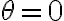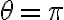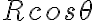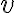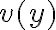MecNew: Pregunta teórica sobre III.6)

En el ejercicio 6 del práctico 3 se pide en un momento encontrar la energía potencial U y luego estudiar los puntos de equilibrio y estabilidad.

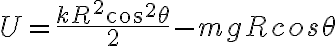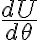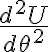Una forma de expresar el potencial es $U = \frac{kR^2cos^2\theta}{2} - mgRcos\theta$ , que es la que aparece en el video. Ahí, al estudiar $\frac{dU}{d\theta}$ y $\frac{d^2U}{d\theta ^2}$ se encuentran los puntos de equilibrio con las características que aparecen en los resultados.

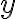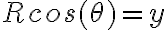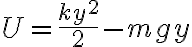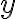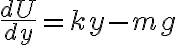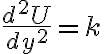Sin embargo, tambien podría, si le llamo $y$ a la distancia del radio horizontal del círculo al punto (es decir, al largo del resorte), que cumple $Rcos(\theta) = y$ se puede escribir U como $U = \frac{ky^2}{2} - mgy$ , que es más sencilla. En teoría $y$ parece una variable super natural para el problema, pero si estudio $\frac{dU}{dy} = ky - mg$ y $\frac{d^2U}{dy^2} = k$ no me aparece el caso de equilibrio 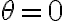$\theta = 0$ , equivalente a 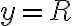$y = R$ (y si apareciera, sería estable). Además aparece solo una solución que corresponde a dos 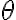$\theta$ distintos, pero eso es razonable.

Yo de hecho hice el ejercicio de esta segunda forma la primera vez porque era matemáticamente más sencillo y me salteé un estado de equilibrio. Para evitarlo a futuro ¿Cómo puedo saber en general si estoy usando la variable correcta para mi problema?

Re: Pregunta teórica sobre III.6)

de Telmo Canabarro - jueves, 23 de abril de 2020, 20:49

Hola, cómo estás Santiago?

Te animas a compartir como te queda la ecuación de movimiento con ese cambio de variable?

Si miras la página 44 de los apuntes o la página 17 de la presentación utilizada en la clase del martes 14 de abril podras observar que no imponemos directamente que la derivada del potencial respeto a theta sea cero sino que identificamos que al imponer condiciones de equilibrio en la ecuación del movmiento dicha derivada es cero.

Re: Pregunta teórica sobre III.6)

de Ariel Fernández - viernes, 24 de abril de 2020, 02:26

Hola,

sin abundar en muchos detalles de análisis matemático, vayamos directo a la intuición física que es lo que queremos desarrollar en este curso lo más posible: con la especificación de $y$ no estás dando correctamente una sola posición de la partícula y por lo tanto no es un grado de libertad del sistema ( $y=Rcos\theta$ se corresponde con dos posibles ángulos y eso acarrea problemas al estudiar una posición de equilibrio como es el punto más bajo de la guía [que ya te dice Newton fácilmente que es de equilibrio]). Las buenas coordenadas para tratar los problemas de mecánica, como es el caso de $\theta$ , no son ambiguas.

DIcho lo anterior, no nos deshagamos completamente de la tentación de usar $y$ y coservémosla por un momento como variable auxiliar, sabiendo que depende de la coordenada $\theta$ del sistema; podemos escribir entonces $U$ tal como lo hacés vos:

$U(\theta)=\frac{ky^2}{2}-mgy$ , con $y=y(\theta)$ .

Luego, las posiciones de equilibrio del sistema se pueden hallar a partir de $\frac{dU}{d\theta}=0$ (que como bien te dice Telmo en su respuesta se corresponden con el análisis de la ecuación de movimiento escrita en términos de $\theta$ ), que podés hacer en dos pasos siguiendo la regla de la cadena:

$\frac{dU}{d\theta}=\frac{dU}{dy}\frac{dy}{d\theta}=0$

de donde ves que tenés posiciones de equilibrio para los ángulos que hacen $\frac{dU}{dy}=0$ (como el que hallaste vos) pero TAMBIÉN para los que hacen $\frac{dy}{d\theta}=0$ , que corresponden a $\theta=0$ ( $\theta=\pi$ también si analizáramos además el movimiento en el tramo superior de la guía). Usando $\theta$ de entrada te aparecen los mismos juegos de posiciones de equilibrio pero de forma más natural digamos.

El estudio de la estabilidad se puede hacer también manteniendo la variable $y$ (lo hice por tranquilidad matemática!) y es un poco más engorroso que el estudio usual pero coherente. De todas formas, la sugerencia en este punto es volver al primer párrrafo y elegir una buena coordenada.

Saludos,

Ariel.

Re: Pregunta teórica sobre III.6)

de Santiago Alejandro Bosch Roascio - viernes, 24 de abril de 2020, 08:09

Muchas gracias por las aclaraciones! Creo que entendí

De hecho, cuando estudié la ecuación de movimiento reemplacé $y$ por $Rcos \theta$ porque era más clara la relación con $v$ , así que no se cómo quedaría bien. Solamente traté con $y$ después porque, al no tener que preocuparme por $v(y)$ , me parecía más fácil así.