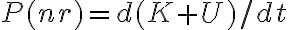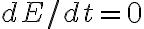Me parece que tu pregunta está en el foro equivocado, porque es una pregunta sobre el práctico IV de Movimiento Central.
Respecto a la primer parte de tu pregunta (pregunta A), para el caso de un movimiento central en que el sistema sea conservativo, si al derivar respecto al tiempo el teorema de conservación de la energía se obtiene la componente radial de la ecuación de Newton, la respuesta es si. La demostración está en las páginas 4 y 5 de los Apuntes R Marotti Movimiento Central, donde se deduce la componente radial de la ecuación de Newton y se deriva respecto al tiempo el teorema de la energía y dan lo mismo.
Respecto a la pregunta B, la primer acotación es que la ecuación que vos escribís ya está derivada respecto al tiempo y sería esa ecuación la que correspondería a la ecuación de movimiento. Y otra acotación es que hablás de fuerzas no residuales. ¿Qué son las fuerzas no residuales? Tal vez querés decir las fuerzas residuales que son las no conservativas, que sería en el caso que no vale el teorema de conservación de la energía. Y la igualdad valdrá en caso que se trate de un movimiento central, es decir, la fuerza no conservativa es radial. La demostración es igual a la anterior introduciendo una fuerza radial no conservativa.
Si la fuerza no es radial (no tenemos un movimiento central) ahí se complica, porque ya no vale la conservación del momento angular. Y en general cuando tengo más de un grado de libertad la derivación del teorema general de la energía da lugar a una combinación lineal de las ecuaciones de movimiento que se tengan, que son más de una si tengo más de un grado de libertad.