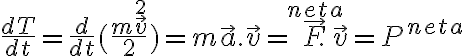Foro Práctico III

No hay problema con simplificar el 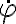$\dot{ \varphi }$ al hallar la ecuación de movimiento, y luego hacerlo cero al hallar el equilibrio. Ese 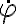$\dot{ \varphi }$ que simplificaste es lo que se llama la solución introducida al demostrar el teorema de la energía. No es una solución de la ecuación de movimiento. 

En efecto, el primer paso para deducir el teorema de la energía es derivar respecto al tiempo la energía cinética y luego usar la segunda ley de Newton: 

$\frac{dT}{dt} = \frac{d}{dt} ( \frac{m \vec{v}^2 }{2} ) = m \vec{a}. \vec{v} = \vec{F}^{neta}. \vec{v} = P^{neta}$

donde T es la energía cinética, 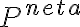$P^{neta}$ es la potencia de la fuerza neta 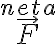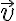$\vec{F}^{neta}$, $\vec{v}$ la velocidad y 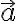$\vec{a}$ la aceleración. Lo que esencialmente falta para deducir el teorema general de la energía es integrar en el tiempo esta ecuación y hacer aparecer el trabajo. Luego en un sistema conservativo el trabajo es menos la variación de la energía potencial. 

O sea que básicamente al demostrar el teorema de la energía se parte de multiplicar escalarmente la segunda ley de Newton por la velocidad, y luego se integra en el tiempo. Eso es por lo que cada vez que hallemos una ecuación de movimiento derivando respecto al tiempo el teorema de la energía (paso inverso a su demostración) nos aparece la velocidad multiplicando. Que podemos simplificar, porque la pusimos allí al demostrar el teorema de la energía. En este ejercicio la velocidad es esencialmente 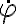 $\dot{ \varphi }$, a menos de un factor multiplicativo.

Pero la ecuación de movimiento es más general que el equilibrio. Vale siempre. En particular si hay equilibrio.