Hola buenas tardes,
No estaría pudiendo hallar los puntos de equilibrio en este ejercicio, quería pedir algun consejo de por donde encararlo.
Gracias.
Hola buenas tardes,
No estaría pudiendo hallar los puntos de equilibrio en este ejercicio, quería pedir algun consejo de por donde encararlo.
Gracias.
Para hallar las posiciones de equilibrio en este Ejercicio hay dos formas.
La primera forma es partiendo de la ecuación de movimiento, hacer la aceleración angular nula. Esto es porque por definición el equilibrio es la posición en que si yo pongo la partícula con velocidad nula, ella se queda allí. Para ello entonces tengo que hacer velocidad y aceleración nulas (porque si la aceleración es no nula, o la velocidad es no nula, la partícula se moverá). Pero como en la ecuación de movimiento solo aparece la aceleración angular, alcanza con hacer esta nula.
La segunda forma es hallar una energía potencial efectiva (o sea, encontrar una ley de conservación de la energía con una energía potencial efectiva), y hallar los extremos relativos de esta energía potencial efectiva. Allí estarán las posiciones de equilibrio.
Para hallar esta energía potencial efectiva, también hay dos formas. Una es directamente preintegrar la ecuación de movimiento. Esa preintegral corresponde a una ley de conservación de la energía.
La otra, que lleva al mismo resultado, es ver que este Ejercicio está en las condiciones del Ejercicio No 9 (resuelto en la página EVA) y que entonces se conserva la energía en el sistema relativo donde la fuerza ficticia centrífuga introduce un potencial como el de la parte a de dicho Ejercicio.
La ventaja de introducir la energía potencial efectiva (sea por comparación con el Ejercicio 9, o preintegrando) es que ya nos va a permitir hacer la parte c de estudio de la estabilidad de las posiciones de equilibrio. Los mínimos son estables, los máximos son inestables. Me refiero a mínimos y máximo de la energía potencial efectiva.
Hola, estoy intentando resolver la parte b), y no comprendo como llegar a la conclusion de que estamos en las condiciones del Ejercicio 9.
Mi duda es que en este caso no entiendo como la potencia de la aceleración de coriolis es cero, dado que si bien la fuerza de coriolis es perpendicular a la velocidad relativa, no pasa lo mismo con la velocidad de transporte( velocidad que tiene la partícula por moverse alrededor del eje OC).
Una posible forma de resolver la duda viene a raíz de haber planteado la segunda Ley de newton, en la que observe que la fuerza de coriolis debía ser igual y opuesta a una reacción de la guía circular (ambas perpendiculares al plano de la guia) esto tiene sentido debido a que la partícula siempre se mantiene en el plano de la guía circular. Es esta la razón por la que la fuerza de coriolis no genera ningún potencial?
Desde ya gracias.
La razón por la que la fuerza de Coriolis es de potencia nula, es que en el sistema relativo su potencia es:
por lo que el producto escalar es nulo porque 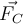 es perpendicular a
es perpendicular a 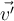 .
.
O sea, cuando me paro en el sistema relativo el cálculo de la potencia relativa involucra la velocidad relativa solamente (y no la velocidad absoluta, por lo que el término de arrastre o transporte no aparece).
Esto es porque a la hora de demostrar el teorema de la energía en el sistema relativo parto de la energía cinética relativa:
Luego derivo esta energía:
En tu razonamiento vos estás mezclando cantidades medidas en el sistema relativo (fuerza de Coriolis, que no existe en el sistema absoluto) con cantidades medidas en el sistema absoluto (velocidad de arrastre).
La reacción de la guía también es de potencia nula en el sistema relativo, (no lo es en el sistema absoluto) porque su potencia relativa involucra también la velocidad relativa que es tangente a la guía (y la reacción es normal por ser la guía lisa).
En el sistema absoluto esta reacción no es de potencia nula porque ahí si importa el término de arrastre.
Podés ver estos detalles en la resolución del Ejercicio III.9.
Hola,
antes que nada te recomiendo que veas los Apuntes 2010, sección 3.3.1 y si querés veas la clase 11 de OpenFING para ampliar, se trata del caso del Ej 9d) pero todo lo que se ve ahí es generalizable.
Para el ejercicio 11 en concreto, si planteás la 2da ley de Newton (para lo cual necesitás la aceleración de la partícula vista desde un referencial inercial, etc) y proyectás según la dirección tangente a la guía, la ecuación de movimiento a la que llegás es de la forma:
siendo 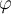 el ángulo que te permite ubicar a la partícula sobre el aro (indicado en la figura del ejercicio).
el ángulo que te permite ubicar a la partícula sobre el aro (indicado en la figura del ejercicio).
Esta ecuación es preintegrable (multiplicás la anterior por 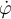 , etc.) y se llega a:
, etc.) y se llega a:
siendo 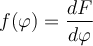 . Más allá de factores dimensionales, el primer término del lado izquierdo tiene la forma de una energía cinética (de hecho es la energía cinética relativa a la guía que te explicaba antes Ricardo) y el segundo es una función del grado de libertad
. Más allá de factores dimensionales, el primer término del lado izquierdo tiene la forma de una energía cinética (de hecho es la energía cinética relativa a la guía que te explicaba antes Ricardo) y el segundo es una función del grado de libertad 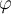 del sistema, por lo que toma en esta suerte de ecuación de conservación, el rol de una energía potencial (suma de la energía potencial de las fuerzas activas -en este caso la elástica- y el potencial de la fuerza de transporte
del sistema, por lo que toma en esta suerte de ecuación de conservación, el rol de una energía potencial (suma de la energía potencial de las fuerzas activas -en este caso la elástica- y el potencial de la fuerza de transporte 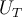 ), mientras que la constante del lado derecho representa la cantidad conservada, es decir una suerte de energía (la energía mecánica de la partícula relativa al sistema móvil). Para esta interpretación no necesitás saber las aclaraciones entre paréntesis que te hago en la frase anterior, alcanza con identificar que algo que va con el cuadrado de la derivada de la coordenada con que ubicás a la partícula es una función no nula suficiente a efectos del equilibrio y estabilidad, mientras que la función
), mientras que la constante del lado derecho representa la cantidad conservada, es decir una suerte de energía (la energía mecánica de la partícula relativa al sistema móvil). Para esta interpretación no necesitás saber las aclaraciones entre paréntesis que te hago en la frase anterior, alcanza con identificar que algo que va con el cuadrado de la derivada de la coordenada con que ubicás a la partícula es una función no nula suficiente a efectos del equilibrio y estabilidad, mientras que la función 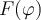 sumada a ella cumple también a efectos de equilibrio y estabilidad el rol de una energía potencial.
sumada a ella cumple también a efectos de equilibrio y estabilidad el rol de una energía potencial.
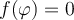 ya da las posiciones de equilibrio por ser la derivada de la función potencial y el estudio de la derivada primera de
ya da las posiciones de equilibrio por ser la derivada de la función potencial y el estudio de la derivada primera de  en las posiciones de equilibrio nos da la información acerca de la estabilidad de las mismas.
en las posiciones de equilibrio nos da la información acerca de la estabilidad de las mismas.